To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fractional vorticesProduct highlight
DefinitionThe term Fractional vortex is used for various quantum vortices or topological defects in different physical systems and in different contexts when these vortices have either phase winding different from Vortices on grain boundaries in d-wave superconductors and Josephson JunctionsIn context of d-wave superconductivity, a Fractional vortex known also as splinter vortex is a vortex of supercurrent carrying unquantized magnetic flux, in oppose to conventional Josephson vortex and semifluxons. Fractional vortices exist in the so-called 0-π long Josephson junctions dense chains. Fractional vortices are solitons which are able to move and preserve their shape much like conventional Josephson vortices and in opposed to semifluxons which are attached to the boundary between 0 and π regions. Theoretically one can obtain an effective double sin-Gordon equation for the phase difference between the two superconducting banks of the 0-π long Josephson junctions dense chains. This is done by taking the asymptotic expansion of the phase difference equation of motion to the second order which results in
where γ is a dimensionless constant defined by the junction's properties. The detailed mathematical procedure is similar to the one done for a parametrically driven pendulum, see for example[1] and [2] , and can be extended to time dependent phenomena[3]. For γ > 1 he above equation for the phase, ψ, has two stable equilibrium values ψγ = cos(1 / γ) and − ψγ. There are two fractional vortices which correspond to these two values one carries Φ1= ψγΦ0/π flux and the other carries Φ2= Φ0-Φ1 flux where Φ0 is the fundamental unit of magnetic flux quantum. For the first time fractional vortices were observed using d-wave superconductors at asymmetric 45° grain boundaries YBa2Cu3O7-δ . In these systems the phase shift of π takes place inside the d-wave superconductor and not at the barrier. Due to the advent of controlled coupling by proper chosen ferromagnetic thicknesses, 0–π JJs have also recently been realized in low-Tc SFS-like systems [4] and underdamped SIFS-type [5]. SuperfluidityIn certain states of spin-1 superfluids or Bose condensates condensate's wavefunction is invariant if to change a superfluid phase by π, along with a π rotation of spin angle. This is in contrast to 2π invariance of condensate wavefunction in a spin-0 superfluid. A vortex resulting from such phase windings is called fractional or half-quantum vortex, in contrast to one-quantum vortex where a phase changes by 2π [6]. Multicomponent superconductivity and metallic superfluidityThe term "Fractional vortex" appears also in context of multicomponent superconductivity of e.g. in the theories of the projected quantum states of liquid metallic hydrogen, where two order parameters originate from theoretically anticipated coexistence of electronic and protonic superconductivity. There a topological defects with an 2π (i.e. "integer") phase winding only in electronic or only in protonic condensate carries fractionally quantized magnetic flux and superfluid momentum and is called "fractional flux vortex" [7]. See alsoReferences
and
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fractional_vortices". A list of authors is available in Wikipedia. |





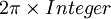 or carry nonquantized or fractionally quantized magnetic field.
or carry nonquantized or fractionally quantized magnetic field.