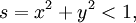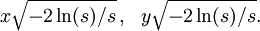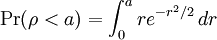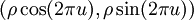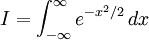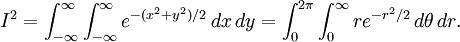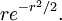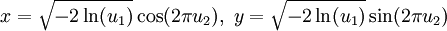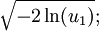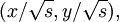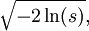My watch list

Marsaglia polar method

In computer science – in particular, in applications of the Monte Carlo method – the Marsaglia polar method is a method for generating a pair of independent standard normal random variables by choosing random points (x, y) in the square −1 < x < 1, −1 < y < 1 until

$s=x^2+y^2 < 1, \,$

Additional recommended knowledge

What is the Sensitivity of my Balance?

Daily Sensitivity Test

Essential Laboratory Skills Guide

and then returning the required pair of normal random variables as

$x\sqrt{-2\ln(s)/s}\,,\ \ y\sqrt{-2\ln(s)/s}.$

Theoretical basis

The underlying theory may be summarized as follows.

If u is uniformly distributed in the interval 0 ≤ u < 1, then the point (cos(2πu), sin(2πu)) is uniformly distributed on the unit circumference x² + y² = 1, and multiplying that point by an independent random variable ρ whose distribution is

$\Pr(\rho<a)=\int_0^a re^{-r^2/2}\,dr$

will produce a point

$\left(\rho\cos(2\pi u),\rho\sin(2\pi u)\right)$

whose coordinates are jointly distributed as two independent standard normal random variables.

History

This idea dates back to Laplace, whom Gauss credits with finding

$I=\int_{-\infty}^\infty e^{-x^2/2}\,dx$

by taking the square root of

$I^2 = \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)/2}\,dx\,dy =\int_0^{2\pi}\int_0^\infty re^{-r^2/2} \, d\theta \, dr.$

The transformation to polar coordinates makes evident that θ is uniformly distributed (constant density) from 0 to 2π, and that the radial distance r has density

$re^{-r^2/2}.$

(Note that r² has the appropriate chi square distribution.)

This method of producing a pair of independent standard normal variates by radially projecting a random point on the unit circumference to a distance given by the square root of a chi-square-2 variate is called the polar method for generating a pair of normal random variables,

Practical considerations

A direct application of this idea,

$x=\sqrt{-2\ln(u_1)}\cos(2\pi u_2),\ y=\sqrt{-2\ln(u_1)}\sin(2\pi u_2)$

is called the Box Muller transform, in which the chi variate is generated as

$\sqrt{-2\ln(u_1)};$

but that transform requires logarithm, square root, sine and cosine functions.

The Marsaglia polar method, in which a random point (x, y) inside the unit circle is projected onto the unit circumference by setting s = x² + y² and forming the point

$(x/\sqrt{s},y/\sqrt{s}),$