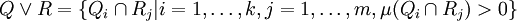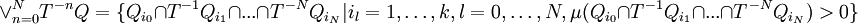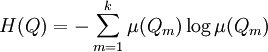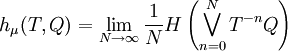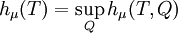To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Measure-preserving dynamical systemIn mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular. Product highlight
DefinitionA measure-preserving dynamical system is defined as a probability space and a measure-preserving transformation on it. In more detail, it is a system with the following structure:
This definition can be generalized to the case in which T is not a single transformation that is iterated to give the dynamics of the system, but instead is a monoid (or even a group) of transformations
The earlier, simpler case fits into this framework by defining Ts: = Ts for ExamplesExamples include:
DiscussionOne may wonder why the seemingly simpler identity
is not used. Here is the problem: suppose T : [0, 1] → [0, 1] is defined by T(x) = (4x mod 1), i.e., T(x) is the "fractional part" of 4x. Then the interval [0.01, 0.02] is mapped to an interval four times as long as itself, but nonetheless the measure of T −1( [0.04, 0.08] ) = [0.01, 0.02] ∪ [0.26, 0.27] ∪ [0.51, 0.52] ∪ [0.76, 0.77] is no different from the measure of [0.04, 0.08]. That hypothesis suffices for the proofs of ergodic theorems. This transformation is measure-preserving. HomomorphismsThe concept of a homomorphism and an isomorphism may be defined. Consider two dynamical systems is a homomorphism of dynamical systems if it satisfies the following three properties:
The system The map φ is an isomorphism of dynamical systems if, in addition, there exists another mapping that is also a homomorphism, which satisfies
Generic pointsA point Symbolic names and generatorsLet
The set of symbolic names with respect to a partition is called the symbolic dynamics of the dynamical system. A partition Q is called a generator or generating partition if μ-almost every point x has a unique symbolic name. Operations on partitionsGiven a partition Further, given two partitions With these two constructs we may define refinement of an iterated pullback which plays crucial role in the construction of the measure-theoretic entropy of a dynamical system. Measure-theoretic entropyThe entropy of a partition Q is defined as The measure-theoretic entropy of a dynamical system Finally, the measure-theoretic entropy of a dynamical system where the supremum is taken over all finite measurable partitions. A theorem of Ya. Sinai in 1959 shows that the supremum is actually obtained on partitions that are generators. Thus, for example, the entropy of the Bernoulli process is log2, since every real number has a unique binary expansion. That is, one may partition the unit interval into the intervals [0,1 / 2) and [1 / 2,1]. Every real number x is either less than 1/2 or not; and likewise so is the fractional part of 2nx. If the space X is endowed with a metric, then the topological entropy may also be defined. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Measure-preserving_dynamical_system". A list of authors is available in Wikipedia. |





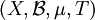
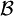 is a σ-algebra over
is a σ-algebra over ![\mu:\mathcal{B}\rightarrow[0,1]](images/math/e/5/5/e550845023c26802da3a36f74e5e98d4.png) is a probability measure, so that
is a probability measure, so that 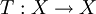 is a measurable transformation which preserves the measure
is a measurable transformation which preserves the measure 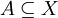 satisfies
satisfies
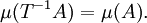
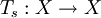 parametrized by
parametrized by 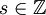 (or
(or 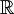 , or
, or 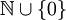 , or
, or 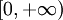 ), where each transformation
), where each transformation 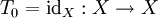 , the identity function on
, the identity function on 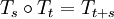 , whenever all the terms are well-defined;
, whenever all the terms are well-defined;
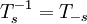 , whenever all the terms are well-defined.
, whenever all the terms are well-defined.
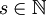 .
.
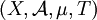 and
and 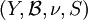 . Then a mapping
. Then a mapping
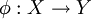
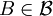 , one has
, one has 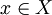 , one has
, one has 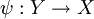
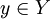 , one has
, one has 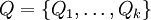 be a partition of X into k measurable pair-wise disjoint pieces. Given a point
be a partition of X into k measurable pair-wise disjoint pieces. Given a point 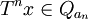 .
.
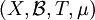 , we define
, we define
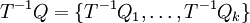
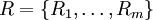 , we define their refinement
, we define their refinement 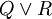 as
as