To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Monte Carlo method in statistical physicsMonte Carlo in statistical physics refers to the application of the Monte Carlo method to problems in statistical physics, or statistical mechanics. Product highlight
Simple samplingFor simplicity, let us consider the statistical mechanics NVT ensemble. The internal energy U of the system is given as a function of the states of all the particles in the system {ri} (this can be the positions for a fluid, or the spin variables in a magnet). Boltzmann statistics establish that the probability of the system be in some state is proportional to
It therefore follows that the average value of any quantity that likewise depends on the states A = A({ri}) can be calculated as
where the normalizing factor is the partition function
which takes care of the lack of normalization of the probability distribution. (Indeed, one sees that the average of any constant number < a > = a, as is sensible). One possible approach is then to exactly enumerate all possible configurations of the system, and calculate averages at will. This is actually done in exactly solvable systems, and in simulations of simple systems with few particles. In realistic systems, on the other hand, even an exact enumeration can be difficult to implement (specially for off-lattice systems). One then may recur to the Monte Carlo method and generate configurations at random. The problem with this approach is that the states that typically contribute with sizable probabilities have a small measure (in the mathematical sense). This method has been likened to calculating the length of the River Nile by considering a set of point on top of a map of Northern Africa (Frenkel and Smit, reference below.) Biased samplingTherefore, the Metropolis algorithm is typically employed. The core of the method is the generation of states that obey Boltzmann probabilities. Any average quantity thus sampled is then, by construction, the statistical average that is sought:
where Aj is the value of A at step j, and N is the total number of steps simulated. The algorithm employs a Markov chain procedure in order to determine a new state for a system from a previous one. According to its stochastic nature, this new state is accepted at random, with an acceptance probability that depends on the Boltzmann factor of the energy increment. i.e., if the trial state has an energy Unew, and the previous had an energy Uold, the criterion of acceptance depends on p = exp[ − (Unew − Uold) / kBT] A very high value of Unew will then lead to a very small p, whereas a very small (negative) one will lead to a high p. In order to fully prescribe an algorithm, a basic condition of balance must be satisfied in order equilibrium be properly described, but detailed balance, a stronger condition, is usually imposed. A typical choice is
CriticismThe method thus neglects dynamics, which can be a major drawback, or a great advantage. Indeed, the method can only be applied to static quantities, but the freedom to choose moves makes the method very flexible. An additional advantage is that some systems, such as the Ising model, lack a dynamical description and are only defined by an energy prescription; for these the Monte Carlo approach is the only one feasible.
See alsoReferences
Categories: Computational chemistry | Theoretical chemistry |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Monte_Carlo_method_in_statistical_physics". A list of authors is available in Wikipedia. |





![P(\{r_i\}) \propto \exp [ - U(\{r_i\}) / k_B T ]](images/math/2/5/5/2558011a6b3174bf7d8950f274788e50.png) .
.
![<A>=\frac{ \sum_{\{r_i\}} A(\{r_i\}) \exp [ - U(\{r_i\}) / k_B T ] } {Z}](images/math/0/c/f/0cf5024ca4c46dcb855d35779289d0f8.png) ,
,
![Z= \sum_{\{r_i\}} P(\{r_i\}) = \sum_{\{r_i\}} \exp [ - U(\{r_i\}) / k_B T ]](images/math/b/8/0/b80c09a9ad05214e6f96b8d2bc12cd2d.png) .
.
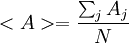 ,
,


