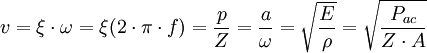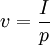My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Particle velocity



Sound measurements
Sound pressure p
Sound pressure level (SPL)
Particle velocity v
Particle velocity level (SVL)
   (Sound velocity level)
Particle displacement ξ
Sound intensity I
Sound intensity level (SIL)
Sound power Pac
Sound power level (SWL)
Sound energy density E
Sound energy flux q
Acoustic impedance Z
Speed of sound c


Particle velocity is the velocity v of a particle (real or imagined) in a medium as it transmits a wave. In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string.
When applied to a sound wave through a medium of air, particle velocity would be the physical speed of an air molecule as it moves back and forth in the direction the sound wave is travelling as it passes.

Particle velocity should not be confused with the speed of the wave as it passes through the medium, i.e. in the case of a sound wave, particle velocity is not the same as the speed of sound.
In applications involving sound, Particle velocity is usually measured using a logarithmic decibel scale called particle velocity level.

Equations in terms of other measurements

The velocity v can be related to the particle displacement ξ and acceleration for single frequency plane wave of frequency f using

v = \xi\cdot \omega = \xi(2 \cdot \pi \cdot f) = \frac{p}{Z} = \frac{a}{\omega} = \sqrt{\frac{E}{\rho}} = \sqrt{\frac{P_{ac}}{Z \cdot A}}

It is further related to the instantaneous acoustic intensity vector I (not the time-averaged averaged acoustic intensity) according to

v = \frac{I}{p}
Symbol Units Meaning
v m/s particle velocity
ξ m, meters particle displacement
ω = 2πf radians/s angular frequency
f Hz, hertz frequency
p Pa, pascals sound pressure
Z N·s/m³ acoustic impedance
E W·s/m³ sound energy density
Pac W, watts sound power or acoustic power
A m² area
a m/s² particle acceleration

See also

  • Sound particle
  • Particle displacement
  • Particle acceleration
  • Pressure gradient
 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Particle_velocity". A list of authors is available in Wikipedia.
Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE