To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Percolation theoryIn mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation. Product highlight
IntroductionA representative question (and the source of the name) is as follows. Assume we have some porous material and we pour some liquid on top. Will the liquid be able to make its way from hole to hole and reach the bottom? We model the physical question mathematically as a three-dimensional network of As is quite typical, it is actually easier to examine infinite networks than just large ones. In this case the corresponding question is: does an infinite open cluster exist? That is, is there a path of connected points of infinite length "through" the network. In this case we may use Kolmogorov's zero-one law to see that, for any given p, the probability that an infinite cluster exists is either zero or one. Since this probability is increasing (this is obvious intuitively, but mathematicians need a coupling argument to prove it), there must be a critical p (denoted by pc) below which the probability is always 0 and above which the probability is always 1. In practice, this criticality is very easy to observe. Even for n as small as 100, the probability of an open path from the top to the bottom increases sharply from very close to zero to very close to one in a short span of values of p. In some cases pc may be calculated explicitly. For example, for the square lattice in two dimensions, pc = 1 / 2, a fact which was an open question for more than 20 years and was finally resolved by Harry Kesten in the early '80s. More often than not, pc cannot be calculated. For example, pc is not known in three dimensions. However, it turns out that calculating pc is not necessarily the most interesting thing to do. The universality principle states that the value of pc is connected to the local structure of the graph, while the behavior of clusters below, at and above pc are invariants of the local structure, and therefore, in some sense are more natural quantities to consider. Sometimes it is easier to open and close vertices rather than edges. This is called site percolation while the model described above is more properly called bond percolation. The subcritical and supercritical phasesFor p < pc, the probability that a specific point (for example, zero) is contained in an open cluster of size r drops exponentially in r. There is, with probability one, one infinite closed cluster. The finite closed clusters, like the open clusters, have exponential tails and thus are very small. Thus the subcritical phase may be described as open islands in a closed sea. The base of the exponent converges to one as p approaches pc. When p > pc just the opposite occurs, with closed islands in an open sea. These facts were proved by Mikhail Menshikov in 1986 and independently by Michael Aizenman and David Barsky in 1987. The critical phaseArguments from quantum field theory and quantum gravitation make a sequence of impressive conjectures about the critical phase, most of which are unproved:
In dimension ≥ 19, these facts (except universality) are proved. In dimension 2, the first fact ("no percolation in the critical phase") is proved for all lattices, but the rest have only been proved for site percolation on the honeycomb or hexagonal lattice, and of course, universality is not proved. In dimensions 3 to 18, even the first conjecture is still open. The different models
See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Percolation_theory". A list of authors is available in Wikipedia. |





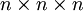 points (or vertices) the connections (or edges) between each two neighbors may be open (allowing the liquid through) with probability p, or closed with probability 1–p, and we assume they are independent. We ask: for a given p, what is the probability that an open path exists from the top to the bottom? Mostly we are interested in the behavior for large n.
points (or vertices) the connections (or edges) between each two neighbors may be open (allowing the liquid through) with probability p, or closed with probability 1–p, and we assume they are independent. We ask: for a given p, what is the probability that an open path exists from the top to the bottom? Mostly we are interested in the behavior for large n.


