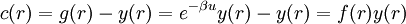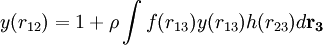To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Percus-Yevick approximationIn statistical mechanics the Percus-Yevick approximation is a closure relation to solve the Ornstein-Zernike equation. It is also referred to as the Percus-Yevick equation. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function. Product highlightDerivationThe direct correlation function represents the direct correlation between two particles in a system containing N − 2 other particles. It can be represented by
where gtotal(r) is the radial distribution function, i.e. g(r) = exp[ − βw(r)] (with w(r) the potential of mean force) and gindirect(r) is the radial distribution function without the direct interaction between pairs u(r) included; i.e. we write gindirect(r) = exp − β[w(r) − u(r)]. Thus we approximate c(r) by
If we introduce the function y(r) = eβu(r)g(r) into the approximation for c(r) one obtains
This is the essence of the Percus-Yevick approximation for if we substitute this result in the Ornstein-Zernike equation, one obtains the Percus-Yevick equation:
See also• Hypernetted Chain equation - another closure relation |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Percus-Yevick_approximation". A list of authors is available in Wikipedia. |





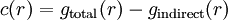
![c(r)=e^{-\beta w(r)}- e^{-\beta[w(r)-u(r)]} \,](images/math/e/b/4/eb483d39f2e7e554cfe031b38e466e2a.png)