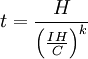To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Peukert's lawPeukert's Law, presented by the German scientist W. Peukert in 1897, expresses the capacity of a lead-acid battery in terms of the rate at which it is discharged. As the rate increases, the battery's capacity decreases, although its actual capacity tends to remain fairly constant. Peukert's law is as follows:
where:
However, more commonly, manufacturers rate the capacity of a battery with reference to a discharge time. Therefore, the following equation should be used:
where H is the hour rating that the battery is specified against and C is the rated capacity at that discharge rate. Note that For an ideal battery, the constant k would equal one, in this case the actual capacity would be independent of the current. For a lead-acid battery, the value of k is typically between 1.1 and 1.3 however. The Peukert constant varies according to the age of the battery generally increasing with age. The Peukert law becomes a key issue in a battery electric vehicle where batteries rated at 20 hour discharges are used at much greater rates of about 1 hour. Watt-hour counters can be programmed with battery capacity, Peukerts exponent, and other particular batteries characteristics. They then count watt-hours and can display various information relating to the state of charge of the battery pack, including remaining energy and thus range. Product highlight
Technical Applications
Example 1Given a Lead Acid class of battery that has been previously tested to determine a Peukert's Exponent of 1.3 you can make the following calculations to determine the possible performance at different discharge rates. At the advertised rate of 200 Ah the battery will produce 200 A·h over a constant period of 20 Hours. Simply put, the battery was designed to discharge at the rate of 10 Amps for 20 Hours. Amps (10) times Hours (20) equals Amp Hours (200). Since everyone sees battery capacity as somewhat likened to water in a glass, one might want to think that the A·h capacity of a battery would remain constant while the Time and Discharge rate remained connected in a linear fashion. This is not the case. Given this same battery under a load of 20A you would think that it would operate for 10 Hours, but it will not, it will operate for only 8.1 Hours. The resulting Ah rating falls to 162.5Ah. An apparent loss of 37.5 Ah or 18.75%. This is the effect of Peukert's law on this particular battery chemistry and structure. Now we have a new starting point. 20A for 10 Hours. If we double the discharge rate to 40A can we expect to see a predictable loss of 18.75%? At 40A we would expect our Peukert adjusted 162.5 A·h battery to operate for 4.06 Hours. Since we already experienced a loss of 18.75% in the first test, after doubling the discharge rate, lets adjust our capacity in this test to see if it falls in line. 18.75% of 162.5Ah is 30.47 A·h. Subtracting this from 162.5 A·h leaves us 132.03 A·h. How close to the mark is our "guestimate"? Pretty darn close. In actuality the battery will test out at 131.96 A·h. Now we have a new mark, a 40A discharge rate produced 132.03 A·h on paper, and very close to that in the real world. If we go to 80 Amps can we expect the same loss of 18.75% from the Peukerts adjusted 132.03 A·h battery? Mathematically we should see 107.29 A·h. In the real world you will see 107.18 A·h. Nearly on the mark! You can now simply create points on your graph for any given battery by testing once, and then extrapolating using the above process. But what about other chemistries? Can the 18.75% rule we just established be used across the board? Let's look at another example. Example 2
Choosing Lithium as our next battery chemistry let's take a look at a 200 A·h cell. Assume the starting test point is the same as the previous case: 10 Amps for 20 Hours, 200 Amp Hours. Now we are going to predict an 18.75% loss in the first step (raising the discharge to 20A) since we experienced that in our first example experiment. Will it fall to 162.5 A·h like the Lead Acid chemistry? No, there is no loss in A·h from the increase in discharge. Likewise there is no loss if we increase the discharge to 40 Amps, another doubling of the discharge. Viewing the chart to the right you will note that there is almost no change in Amp Hour rating over time until you increase the discharge rate to 200 Amps! This is a factor of 1C--in other words, the full capacity of the battery. Taking the discharge to 400 Amps (2C) produces a loss associated to the Peukert law of only 3 Amp Hours. Taking our 1C Peukert adjusted discharge A·h rating of 181 A·h we can see that 3 A·h is a loss of only 1.6%. This percentage will carry though as a constant for all points on the curve up to 11C or a discharge rate of 2,200 Amps. Test ResultsThe results of the tests in the two examples shown illustrate the wide disparity in the Peukert effect on different battery chemistry. The same will be found, but to a lesser degree, with batteries of a different structure, or build, but within the same chemical family. The above tests will allow for you to graph or plot the curves for any battery, and determine the suitability of that particular battery for your needs. According to the charts produced for the two chemistries in the examples, the Lead Acid batteries are very well suited for low discharge current, long duration missions. Lead Acid has a high loss factor when operating at high discharge rates. At only 1C your 200 A·h Lead Acid battery would only have an A·h rating of 81.4 A·h. This is a tremendous cost of operation. Lithium based batteries on the other hand operate well at low currents, or at very high currents. Their advantage though is clearly in the high amperage range, even approaching 11C. The overhead, or loss of A·h, at high C is almost non-existent in Lithium batteries. Testing throughout the charge cycle life of several battery chemistries shows that the Peukert effect remains consistent with the original percentage loss that occurs after doubling the discharge rate. Peukert ApplicationsPeukerts law is nonlinear, and it cannot be applied in advance to future generation batteries. The effect can be best explained as reverse engineering. Build the battery, test it to determine Peukert's effect on that particular chemistry and structure. You can then apply the loss ratio to all batteries of that chemistry and structure at varying capacities. Field ResearchSeveral companies are working to develop technologies that eliminate the Peukert's effect at least within the desired operating range of their batteries. These batteries could then be deemed "perfect" at least for that particular application. Most of this testing is not ready for prime time but there is one company on the web that offers fairly transparent viewing of their ongoing testing. The web site currently shows testing comparisons using an e-bike to compare the effect between several battery technologies. The test fields are updated weekly. Use this link to graph your own battery results for their tests. It is a good exercise in understanding the Peukert Effect. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Peukert's_law". A list of authors is available in Wikipedia. |


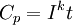
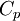 is the capacity according to Peukert, at a one-ampere discharge rate, expressed in A·h.
is the capacity according to Peukert, at a one-ampere discharge rate, expressed in A·h.
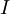 is the discharge current, expressed in
is the discharge current, expressed in 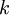 is the Peukert constant, dimensionless.
is the Peukert constant, dimensionless.
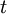 is the time of discharge, expressed in h.
is the time of discharge, expressed in h.