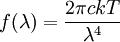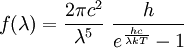To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rayleigh-Jeans law
Product highlightIn physics, the Rayleigh-Jeans Law, first proposed in the early 20th century, attempts to describe the spectral radiance of electromagnetic radiation at all wavelengths from a black body at a given temperature. For wavelength λ, it is; where c is the speed of light, k is Boltzmann's constant and T is the temperature in kelvins. The law is derived from classical physics arguments. Lord Rayleigh first obtained the fourth-power dependence on wavelength in 1900; a more complete derivation, which included the proportionality constant, was presented by Rayleigh and Sir James Jeans in 1905. It agrees with experimental measurements for long wavelengths. However it predicts an energy output that diverges towards infinity as wavelengths grow smaller. This was not supported by experiments and the failure has become known as the ultraviolet catastrophe. In 1900 Max Planck had obtained a different law: where h is Planck's constant. This is Planck's law of black body radiation expressed in terms of wavelength λ = c /ν. The Planck law does not suffer from an ultraviolet catastrophe, and agrees well with the experimental data, but its full significance was only appreciated several years later. In the limit of very high temperatures or long wavelengths, the term in the exponential becomes small, and so the denominator becomes approximately hc /λkT. This gives back the Rayleigh-Jeans Law. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rayleigh-Jeans_law". A list of authors is available in Wikipedia. |