To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Replica trickIn statistical physics of spin glasses and other systems with quenched disorder, the replica trick is a mathematical technique based on the application of the formula Product highlight
The significance of this formula in statistical physics arises when the quantity Z represents the partition function of a system, from which most macroscopic statistical quantities such as entropy, free-energy, heat-capacity, etc, can be calculated. For example, in a spin glass, the pseudo-random interaction between different magnetic dipoles means that the orientation of these dipoles that has lowest energy is very difficult to predict, and is far richer than in an analogous ferromagnetic system. For systems with quenched disorder, one typically expects that macroscopic quantities will be self-averaging, whereby any macroscopic quantity for a specific realization of the disorder will be indistinguishable from the same quantity calculated by averaging over all possible realizations of the disorder. When trying to calculate these macroscopic properties mathematically, it is typically desirable to introduce this average directly into one's calculations by calculating quantities such as
where the angle-brackets represents an average over all realizations of the disorder. Although this average is often extremely difficult to perform directly, an average of the form
is much easier to perform, provided that n is an integer.
In this case, the quantity Zn represents the joint partition function of n identical systems.
The replica trick involves extending this argument to the case where n is no longer constrained to be an integer, by positing that if Zn can be calculated for all positive integers n then this may be sufficient to allow the limiting behaviour as Clearly, such an argument poses many mathematical questions, and the resulting formalism for performing the limit REM: The easiest Replica problemThe Random Energy Model (REM) is one of the simplest models of statistical mechanics of disordered systems, and probably the simplest model to show the meaning and power of the Replica Trick to the level 1 of Replica Symmetry Breaking. The model is especially suitable for this introduction because an exact result by a different procedure is known, and the Replica Trick can be proved to work by crosschecking of results. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Replica_trick". A list of authors is available in Wikipedia. |





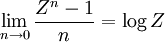
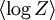
 to be calculated.
to be calculated.


