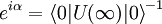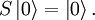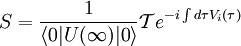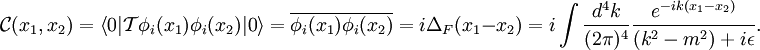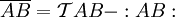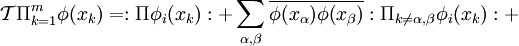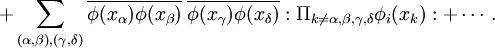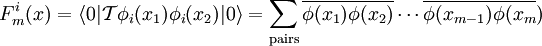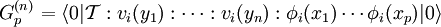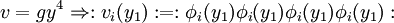To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
S matrix
In physics, the Scattering matrix (S-matrix) relates the initial state and the final state for an interaction of particles. It is used in quantum mechanics, scattering theory and quantum field theory. More formally, the S-matrix is defined as the unitary matrix connecting asymptotic particle states in the Hilbert space of physical states (scattering channels). While the S-matrix may be defined for any background (spacetime) that is asymptotically solvable and has no horizons, it has a simple form in the case of the Minkowski space. In this special case, the Hilbert space is a space of irreducible unitary representations of the inhomogeneous Lorentz group; the S-matrix is the evolution operator between time equal to minus infinity, and time equal to plus infinity. It can be shown that if a quantum field theory in Minkowski space has a mass gap, the state in the asymptotic past and in the asymptotic future are both described by Fock spaces. Product highlight
ExplanationUse of S-matricesThe S-matrix is closely related to the transition probability amplitude in quantum mechanics and to cross sections of various interactions; the elements (individual numerical entries) in the S-matrix are known as scattering amplitudes. Poles of the S-matrix in the complex-energy plane are identified with bound states, virtual states or resonances. Branch cuts of the S-matrix in the complex-energy plane are associated to the opening of a scattering channel. In the Hamiltonian approach to quantum field theory, the S-matrix may be calculated as a time-ordered exponential of the integrated Hamiltonian in the Dirac picture; it may be also expressed using Feynman's path integrals. In both cases, the perturbative calculation of the S-matrix leads to Feynman diagrams. In scattering theory, the S-matrix is an operator mapping free particle in-states to free particle out-states (scattering channels) in the Heisenberg picture. This is very useful because we cannot describe exactly the interaction (at least, the most interesting ones). Mathematical DefinitionIn Dirac notation, we define Now, we define two kinds of creation/destruction operators, acting on different Hilbert spaces (IN space i, OUT space f), So now It is possible to prove that In the Heisenberg picture the states are time-independent, so we can expand initial states on a basis of final states (or vice versa) as follows: Where According to Wigner's theorem, S must be a unitary operator such that
If S describes an interaction correctly, these properties must be also true: If the system is made up with a single particle in momentum eigenstate The S-matrix element must be nonzero if and only if momentum is conserved. S-matrix and evolution operator UTherefore because Substituting the explicit expression for U we obtain: By inspection it can be seen that this formula is not explicitly covariant. LSZ reduction formulaThe LSZ reduction formula is used to calculate predictions of S-matrix elements based on the field being analyzed. Wick's theorem
Wick's theorem is a method of reducing high-order derivatives to a combinatorics problem.(Philips, 2001) It is named after Gian-Carlo Wick. Definition of contraction: Which means that In the end, we approach at Wick's theorem: T Wick's theorem The T-product of a time-ordered free fields string can be expressed in the following manner: Applying this theorem to S-matrix elements, we discover that normal-ordered terms acting on vacuum state give a null contribution to the sum. We conclude that m is even and only completely contracted terms remain. where p is the number of interaction fields (or, equivalently, the number of interacting particles) and n is the development order (or the number of vertices of interaction). For example, if This is analogous to the corresponding theorem in statistics for the moments of a Gaussian distribution. See alsoBibliographyBarut (1967). The Theory of the Scattering Matrix. Tony Philips (11 2001). Finite-dimensional Feynman Diagrams. What's New In Math. American Mathematical Society. Retrieved on 2007-10-23. |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "S_matrix". A list of authors is available in Wikipedia. |





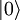 as the vacuum quantum state. If
as the vacuum quantum state. If 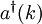 is a creation operator, its hermitian conjugate (destruction or annihilation operator) acts on the vacuum as follows:
is a creation operator, its hermitian conjugate (destruction or annihilation operator) acts on the vacuum as follows:
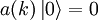
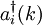 and
and 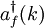 .
.
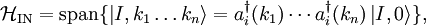
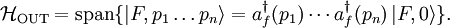
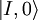 and
and 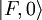 are both invariant under translation and that the states
are both invariant under translation and that the states 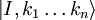 and
and 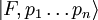 are eigenstates of the momentum operator
are eigenstates of the momentum operator 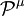 .
.
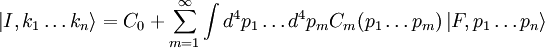
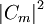 is the probability that the interaction transforms
is the probability that the interaction transforms 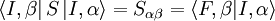 . Moreover,
. Moreover, 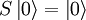
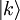 , then
, then 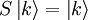
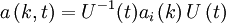
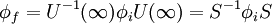
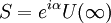 where
where