To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Taylor–Proudman theoremIn fluid mechanics, the Taylor–Proudman theorem (after G. I. Taylor and Joseph Proudman) states that when a solid body is moved slowly within a fluid that is steadily rotated with a high Ω, the fluid velocity will be uniform along any line parallel to the axis of rotation. Ω must be relatively large compared to the movement of the solid body in order to make the coriolis force large compared to the acceleration terms. Product highlightThat this is so may be seen by considering the Navier Stokes equations for steady flow, with zero viscosity and a body force corresponding to the Coriolis force, which are: where where Ω the angular velocity vector. If the curl of this equation is taken, the result is the Taylor–Proudman theorem: To derive this, one needs the vector identities and
Note that The vector form of the Taylor–Proudman theorem is perhaps better understood by expanding it into its coordinate components: Now choose coordinates in which Ωx = Ωy = 0 and then the equations reduce to if |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Taylor–Proudman_theorem". A list of authors is available in Wikipedia. |





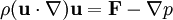
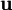 is the fluid velocity,
is the fluid velocity, 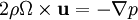
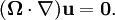
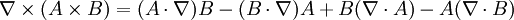
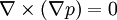 .
.
 is also needed.
is also needed.
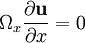
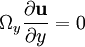
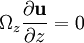
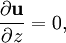
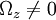 . Note that the implication is that all three components of the velocity vector are uniform along any line parallel to the z-axis.
. Note that the implication is that all three components of the velocity vector are uniform along any line parallel to the z-axis.


