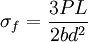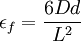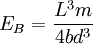To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Three point flexural test
Product highlightTesting MethodCalculation of the flexural stress σf
Calculation of the flexural strain εf
Calculation of Young's modulus EB
in these formulas the following parameters are used:
See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Three_point_flexural_test". A list of authors is available in Wikipedia. |