To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Tribimaximal mixingTribimaximal mixing [1] is a specific postulated form for the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) lepton mixing matrix U. Tribimaximal mixing is defined by a particular choice of the matrix of moduli-squared of the elements of the PMNS matrix as follows: The tribimaximal mixing form is compatible with all verified neutrino oscillation experiments to date,[2] and may be used as a zeroth-order approximation to more general forms for the PMNS matrix e.g.[3][4] which are also consistent with the data. In the standard (PDG[2]) convention for the PMNS matrix, tribimaximal mixing may be specified in terms of lepton mixing angles as follows: Product highlight
Explanation of nameThe name tribimaximal reflects the commonality of the tribimaximal mixing matrix with two previously proposed specific forms for the PMNS matrix, the trimaximal[5] and bimaximal[6] mixing schemes, both now ruled out by data. In tribimaximal mixing,[1] the ν2 neutrino mass eigenstate is said to be "trimaximally mixed" in that it consists of a uniform admixture of νe, νμ and ντ flavour eigenstates, ie. maximal mixing among all three flavour states. The ν3 neutrino mass eigenstate, on the other hand, is "bimaximally mixed" in that it comprises a uniform admixture of only two flavour components, ie. νμ and ντ maximal mixing, with effective decoupling of the νe from the ν3, just as in the original bimaximal scheme.[6] PhenomenologyBy virtue of the zero ( | Ue3 | 2 = 0) in the tribimaximal mixing matrix, exact tribimaximal mixing would predict zero for all CP-violating asymmetries in the case of Dirac neutrinos (in the case of Majorana neutrinos, Majorana phases are still permitted, and could still lead to CP-violating effects). For solar neutrinos the large angle MSW effect in tribimaximal mixing accounts for the experimental data, predicting average suppressions HistoryThe name tribimaximal first appeared in the literature in 2002[1] although this specific scheme had been previously published in 1999[7] as a viable alternative to the trimaximal[5] scheme. Tribimaximal mixing is sometimes confused with other mixing schemes, e.g.[8] which differ from tribimaximal mixing by row- and/or column-wise permutations of the mixing-matrix elements. Such permuted forms are experimentally distinct however, and are now ruled out by data.[2] References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Tribimaximal_mixing". A list of authors is available in Wikipedia. |


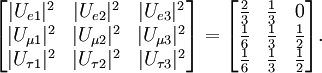
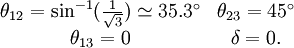



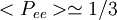 in the Sudbury Neutrino Observatory (SNO) and
in the Sudbury Neutrino Observatory (SNO) and 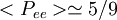 in lower energy solar neutrino experiments (and in long baseline reactor neutrino experiments). The bimaximally mixed
in lower energy solar neutrino experiments (and in long baseline reactor neutrino experiments). The bimaximally mixed 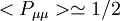 observed for
observed for 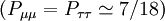 , will be extremely hard to test experimentally.
, will be extremely hard to test experimentally.


