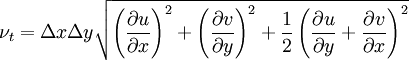To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Turbulence modelingTurbulence modeling is the area of physical modeling where a simpler mathematical model than the full time dependent Navier-Stokes Equations is used to predict the effects of turbulence. Product highlightJoseph Boussinesq was the first practitioner of this, introducing the concept of eddy viscosity. In this model, the additional turbulent stresses are given by augmenting the molecular viscosity with an eddy viscosity. This can be a simple constant eddy viscosity (which works well for some free shear flows such as axisymmetric jets, 2-D jets, and mixing layers). Later, Ludwig Prandtl introduced the additional concept of the mixing length, along with the idea of a boundary layer. For wall-bounded turbulent flows, the eddy viscosity must vary with distance from the wall, hence the addition of the concept of a 'mixing length'. In the simplest wall-bounded flow model, the eddy viscosity is given by the equation:
This simple model is the basis for the "Law of the Wall", which is a surprisingly accurate model for wall-bounded, attached (not separated) flow fields with small pressure gradients. More general turbulence models have evolved over time, with most modern turbulence models given by field equations similar to the Navier-Stokes equations. Among many others, Joseph Smagorinsky (1964) proposed a useful formula for the eddy viscosity in numerical models, based on the local derivatives of the velocity field and the local grid size: References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Turbulence_modeling". A list of authors is available in Wikipedia. |





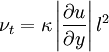
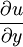 is the partial derivative of the streamwise velocity (u) with respect to the wall normal direction (y);
is the partial derivative of the streamwise velocity (u) with respect to the wall normal direction (y);