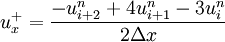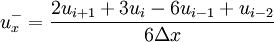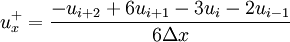To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Upwind schemeIn computational fluid dynamics, the upwind schemes are any of a class of discretization methods to solve hyperbolic partial differential equations numerically. The wave eation, the advection equation, the Euler equations in fluid dynamics, etc. belongs to hyperbolic PDEs. Upwind schemes use an adaptive or solution-sensitive finite difference stencil to numerically simulate more properly the direction of propagation of information in a flow field. More specifically, upwind schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. Historically, the origin of upwind methods can be traced back to the work of Courant, Isaacson, and Reeves who proposed the CIR method. Product highlight
Model equationTo illustrate the method, consider the following one-dimensional linear wave equation It describes a wave propagating in the x-direction with a velocity a. The preceding equation
is also a mathematical model for one-dimensional linear advection. Consider a typical grid point i in the
domain. In a one-dimensional domain, there are only two direction associated with point i - left and
right. If a is positive the left side is called upwind side and right side is the downwind side. Similarly, if a is negative the left side is called downwind side and right side is the upwind side. If the finite difference scheme for the derivative, First-order upwind schemeThe simplest upwind scheme possible is the first-order upwind scheme. It is given by Defining and the two conditional equations (1) and (2) can be combined and written in a compact form as Equation (3) is a general way of writing any upwind-type schemes. The upwind scheme is stable if the following Courant–Friedrichs–Lewy condition (CFL) condition is satisfied. A Taylor series analysis of the upwind scheme discussed above will show that it is first-order accurate in space and time. The first-order upwind scheme introduces severe numerical diffusion in the solution where large gradients exists. Second-order upwind schemeThe spatial accuracy of the first-order upwind scheme can be improved by choosing a more accurate finite difference stencil for the approximation of spatial derivative. For the second-order upwind scheme, and This scheme is less diffusive compared to the first-order accuarte scheme. Third-order upwind schemeFor the third-order upwind scheme, and This scheme is less diffusive compared to the second-order accuarte scheme. However, it is known to introduce slight dispersive errors in the region where the gradient is high. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Upwind_scheme". A list of authors is available in Wikipedia. |





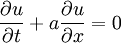
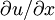 contain more
points in the upwind side, the scheme is called an upwind-biased or simply upwind scheme.
contain more
points in the upwind side, the scheme is called an upwind-biased or simply upwind scheme.
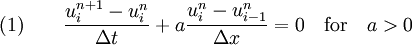
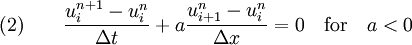

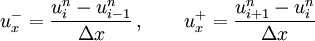
![\quad (3) \qquad u_i^{n+1} = u_i^n - \Delta t \left[ a^+ u_x^- + a^- u_x^+ \right]](images/math/9/d/3/9d31342cc7ed2f65b7a941fc5ba3fdff.png)
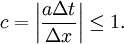
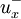 in equation (3) is defined as
in equation (3) is defined as
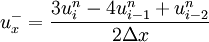
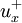 is defined as
is defined as