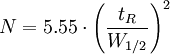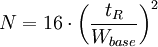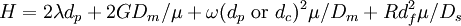To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Van Deemter's equationThe Van Deemter equation in chromatography relates the variance per unit length of a separation column to the linear mobile phase velocity by considering physical, kinetic, and thermodynamic properties of a separation [1] [2]. These properties include pathways within the column, diffusion (axial and longitudinal), and mass transfer kinetics between stationary and mobile phases. In liquid chromatography, the mobile phase velocity is taken as the exit velocity, that is, the ratio of the flow rate in ml/second to the cross-sectional area of the ‘column-exit flow path.’ For a packed column, the cross-sectional area of the column exit flow path is usually taken as 0.6 times the cross-sectional area of the column. Alternatively, the linear velocity can be taken as the ratio of the column length to the dead time. If the mobile phase is a gas, then the pressure correction must be applied. The variance per unit length of the column is taken as the ratio of the column length to the column efficiency in theoretical plates. The Van Deemter equation is a hyperbolic function that predicts that there is an optimum velocity at which there will be the minimum variance per unit column length and, thence, a maximum efficiency. The Van Deemter equation was the result of the first application of rate theory to the chromatography elution process. Product highlight
Van Deemter equationThe Van Deemter equation for the plate height (H) is:
Where
A is equal to the multiple paths taken by the chemical compound, in open tubular capillaries this term will be zero as there are no multiple paths. The multiple paths occur in packed columns where several routes through the column packing, which results in band spreading. B/u is equal to the longitudinal diffusion of the particles of the compound. Cu is equal to the equilibration point. In a column, there is an interaction between the mobile and stationary phases, Cu accounts for this. Plate countThe plate height given as:
with
By using the more practical peak width at half height or with the width at the base of the peak: Expanded van DeemterThe Van Deemter equation can be further expanded to: Where:
Van Deemter's equation indicates that band broadening mechanisms are proportionally dependent on flow rate, inversely proportional to flow rate and independent of flow rate. References |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Van_Deemter's_equation". A list of authors is available in Wikipedia. |





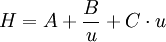
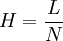
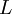 the column length and :
the column length and :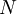 the plate count can be estimated from a chromatogram by analysis of the
the plate count can be estimated from a chromatogram by analysis of the 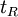 for each component and its standard deviation
for each component and its standard deviation 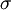 as a measure for peak width, provided that the elution curve represents a Gaussian curve.
as a measure for peak width, provided that the elution curve represents a Gaussian curve.
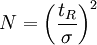
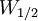 the equation is:
the equation is: