To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
West numberThe West number is an emperical parameter used to characterize the performance of Stirling engines, and other Stirling systems. It is very similar to the Beale number where a larger number indicates higher performance; however, the West number includes temperature compensation. The West number is often used to approximate of the power output of a Stirling engine. The average value is (0.25) [1] for a wide variety of engines, although it may range up to (0.35) [2], particularly for engines operating with a high temperature differential. Product highlightThe West number may be defined as:
To estimate the power output of a new engine design, nominal values are assumed for the West number, pressure, swept volume and frequency, and the power is calculated as follows:
For example, with an absolute temperature ratio of 2, the portion of the equation representing temperature correction equals 1/3. With a temperature ratio of 3, the temperature term is 1/2. This factor accounts for the difference between the West equation, and the Beale equation in which this temperature term is taken as a constant. Thus, the Beale number is typically in the range of 0.10 to 0.15, which is about 1/3 to 1/2 the value of the West number. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "West_number". A list of authors is available in Wikipedia. |





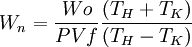
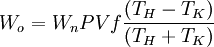 [3]
[3]


