To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Wick rotationIn physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a problem in Minkowski space from a solution to a related problem in Euclidean space, by analytic continuation. Product highlightIt is motivated by the observation that the Minkowski metric
and the four-dimensional Euclidean metric
are equivalent if one permits the coordinate t to take on complex values. The Minkowski metric becomes Euclidean when t is restricted to the imaginary axis, and vice versa. Taking a problem expressed in Minkowski space with coordinates x, y, z, t, and substituting w = it, sometimes yields a problem in real Euclidean coordinates x, y, z, w which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem. Wick rotation connects quantum mechanics to statistical mechanics in a surprising way. The Schrödinger equation and the heat equation are related by Wick rotation, for example. However, there is a slight difference. Statistical mechanics n-point functions satisfy positivity whereas Wick-rotated quantum field theories satisfy reflection positivity. It is called a rotation because when we represent complex numbers as a plane, the multiplication of a complex number by i is equivalent to rotating the vector representing that number by an angle of When Stephen Hawking wrote about "imaginary time" in his famous book A Brief History of Time, he was referring to Wick rotation. Wick rotation also relates a QFT at a finite inverse temperature β to a statistical mechanical model over the "tube" R3×S1 with the imaginary time coordinate τ being periodic with period β. Note, however, that the Wick rotation cannot be viewed as a rotation on a complex vector space that is equipped with the conventional norm and metric induced by the inner product, as in this case the rotation would cancel out and have no effect at all. See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Wick_rotation". A list of authors is available in Wikipedia. |





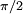 .
.


