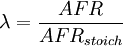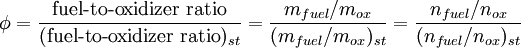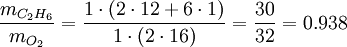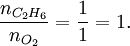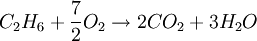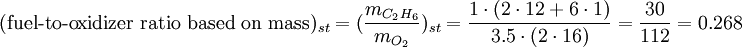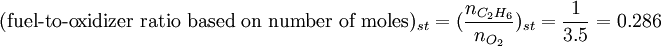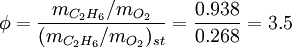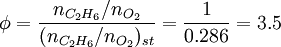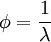To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Air-fuel ratioAir-fuel ratio (AFR) is the mass ratio of air to fuel present during combustion. When all the fuel is combined with all the free oxygen, typically within a vehicle's combustion chamber, the mixture is chemically balanced and this AFR is called the stoichiometric mixture (often abbreviated to stoich). AFR is an important measure for anti-pollution and performance tuning reasons. Lambda (λ) is an alternative way to represent AFR. In industrial fired heaters, power plant steam generators, and large gas-fired turbines, the more common term is percent excess combustion air. For example, excess combustion air of 15 percent means that 15 percent more than the required stoichiometric air is being used. A mixture is the working point that modern engine management systems employing fuel injection attempt to achieve in light load cruise situations. For gasoline fuel, the stoichiometric air/fuel mixture is approximately 14.7 times the mass of air to fuel. Any mixture less than 14.7 to 1 is considered to be a rich mixture, any more than 14.7 to 1 is a lean mixture - given perfect (ideal) "test" fuel (gasoline consisting of solely n-heptane and iso-octane). In reality, most fuels consist of a combination of heptane, octane, a handful of other alkanes, plus additives including detergents, and possibly oxygenators such as MTBE (Methyl tertiary-butyl ether) or ethanol/methanol. These compounds all alter the stoichiometric ratio, with most of the additives pushing the ratio downward (oxygenators bring extra oxygen to the combustion event in liquid form that is released at time of combustions; for MTBE-laden fuel, a stoichiometric ratio can be as low as 14.1:1). Vehicles using an oxygen sensor(s) or other feedback-loop to control fuel to air ratios (usually by controlling fuel volume) will usually compensate automatically for this change in the fuel's stoichiometric rate by measuring the exhaust gas composition, while vehicles without such controls (such as most motorcycles until recently , and cars predating the mid-1980's) may have difficulties running certain boutique blends of fuels (esp. winter fuels used in some areas) and may need to be rejetted (or otherwise have the fueling ratios altered) to compensate for special boutique fuel mixes. Vehicle manufacturers do not provide a means of altering predefined fuel maps making such alterations impossible without replacing the stock ECU with a customizable system. Vehicles using oxygen sensors enable the air-fuel ratio to be monitored by means of an air fuel ratio meter. Lean mixtures produce cooler combustion gases than does a stoichiometric mixture, primarily due to the excessive dilution by unconsumed oxygen and its associated nitrogen. Rich mixtures also produce cooler combustion gases than does a stoichiometric mixture, primarily due to the excessive amount of carbon which oxidises to form carbon monoxide, rather than carbon dioxide. The chemical reaction oxidizing carbon to form carbon monoxide releases significantly less heat than the similar reaction to form carbon dioxide. (Carbon monoxide retains significant potential chemical energy. It is itself a fuel whereas carbon dioxide is not.) Lean mixtures and rich mixtures, when consumed in an internal combustion engine, both produce less power than does the stoichiometric mixture. Similarly, lean mixtures and rich mixtures return poorer fuel efficiency than the best mixture. (The mixture for the best fuel efficiency is slightly different to the stoichiometric mixture.) Product highlight
SynopsisIn theory a stoichiometric mixture has just enough air to completely burn the available fuel. In practice this is never quite achieved, due primarily to the very short time available in an internal combustion engine for each combustion cycle. Most of the combustion process completes in approximately 4-5 milliseconds at an engine speed of 6000 rpm. This is the time that elapses from when the spark is fired until the burning of the fuel air mix is essentially complete after some 80 degrees of crankshaft rotation. Catalytic converters are designed to work best when the exhaust gases passing through them show nearly perfect combustion has taken place. A stoichiometric mixture unfortunately burns very hot and can damage engine components if the engine is placed under high load at this fuel air mixture. Due to the high temperatures at this mixture, detonation of the fuel air mix shortly after maximum cylinder pressure is possible under high load (referred to as knocking or pinging). Detonation can cause serious engine damage as the uncontrolled burning of the fuel air mix can create very high pressures in the cylinder. As a consequence stoichiometric mixtures are only used under light load conditions. For acceleration and high load conditions, a richer mixture (lower air-fuel ratio) is used to produce cooler combustion products and thereby prevent detonation and overheating of the cylinder head. In the typical air to natural gas combustion burner, a double cross limit strategy is employed to insure ratio control. (This method was used in World War 2). The strategy involves adding the opposite flow feedback into the limiting control of the respective gas (air or fuel).This assures ratio control within an acceptable margin. Other terms usedThere are other terms commonly used when discussing the mixture of air and fuel in internal combustion engines. However, “Stoich” is also known as a slang word. AFRThe Air fuel ratio is the most common reference term used for mixtures in internal combustion engines. It is the ratio between the mass of air and the mass of fuel in the fuel-air mix at any given moment. For pure octane the stoichiometric mixture is approximately 14.7:1 or λ of 1.00 exactly. In Naturally Aspirated engines powered by octane, maximum power is frequently reached at AFRs ranging from 12.5 - 13.3:1 or λ of 0.85 - 0.90. FARFuel Air ratio is frequently used in government studies of internal combustion engine and refers to the ratio of fuel to the air, it is 1/AFR. LambdaMost practical AFR devices actually measure the amount of residual oxygen (for lean mixes) or unburnt hydrocarbons (for rich mixtures) in the exhaust gas. Lambda (λ) is the measure of how far from stoichiometry that mixture is. Lambda of 1.0 is at stoichiometry, rich mixtures are less than 1.0, and lean mixtures are greater than 1.0. There is a direct relationship between lambda and AFR. To calculate AFR from a given lambda, multiply the measured lambda by the stoichiometric AFR for that fuel. Alternatively, to recover lambda from an AFR, divide AFR by the stoichiometric AFR for that fuel. This last equation is often used as the definition of lambda: Because the composition of common fuels varies seasonally, and because many modern vehicles can handle different fuels, when tuning, it makes more sense to talk about lambda values rather than AFR. Equivalence ratioThe equivalence ratio of a system is defined as the ratio of the fuel-to-oxidizer ratio to the stoichiometric fuel-to-oxidizer ratio. Mathematically, where, m represents the mass, n represents number of moles, suffix st stands for stoichiometric conditions. TLALI ratio over fuel-to-oxidizer ratio is that it does not have the same dependence as fuel-to-oxidizer ratio on the units being used. For example fuel-to-oxidizer ratio based on mass of fuel and oxidizer is not same as one define based on number of moles. This is not the case for equivalence ratio. The following example can help clarify the point. Consider a mixture of one mole of ethane (C2H6) and one mole of oxygen (O2).
Clearly the two values are not equal. To compare it to the equivalence ratio, we need to determine the fuel-to-oxidizer ratio of ethane and oxygen mixture. For this we need to consider the stoichiometric reaction of ethane and oxygen, This gives, Thus we can determine the equivalence ratio of the give mixture as, or equivalently as, Another advantage of using the equivalence ratio is that ratios greater than one always represent excess fuel in the fuel-oxidizer mixture, than what would be required for complete combustion (stoichiometric reaction), irrespective of the fuel and oxidizer being used. While ratios less than 1 represent a deficiency of fuel or equivalently excess oxidizer in the mixture. This is not the case if one uses fuel-to-oxidizer ratio, which will take different values for different mixtures. It should be noted that equivalence ratio is related to λ (defined previously) as follows, See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Air-fuel_ratio". A list of authors is available in Wikipedia. |