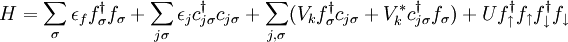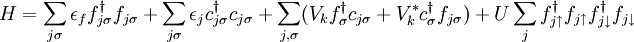My watch list

Anderson model

The Anderson Model is a Hamiltonian model that is often used to describe Heavy Fermion systems. The model contains a narrow resonance between a magnetic impurity state and a conduction electron state. The model also contains a short range U repulsion term as found in the Hubbard model between localized electrons. For a single impurity, the Hamiltonian takes the form

Additional recommended knowledge

What is the Sensitivity of my Balance?

Safe Weighing Range Ensures Accurate Results

Weighing the right way

$H = \sum_{\sigma}\epsilon_f f^{\dagger}_{\sigma}f_{\sigma} + \sum_{j\sigma}\epsilon_j c^{\dagger}_{j\sigma}c_{j\sigma} + \sum_{j,\sigma}(V_k f^{\dagger}_{\sigma}c_{j\sigma} + V_k^* c^{\dagger}_{j\sigma}f_{\sigma}) + Uf^{\dagger}_{\uparrow}f_{\uparrow}f^{\dagger}_{\downarrow}f_{\downarrow}$

where the f operator corresponds to an impurity, and c corresponds to a conduction electron, and $σ$ labels the spin.

In heavy-fermion systems, we find we have a lattice of impurities. The relevant model is then the periodic Anderson model.

$H = \sum_{j\sigma}\epsilon_f f^{\dagger}_{j\sigma}f_{j\sigma} + \sum_{j\sigma}\epsilon_j c^{\dagger}_{j\sigma}c_{j\sigma} + \sum_{j,\sigma}(V_k f^{\dagger}_{\sigma}c_{j\sigma} + V_k^* c^{\dagger}_{\sigma}f_{j\sigma}) + U\sum_{j}f^{\dagger}_{j\uparrow}f_{j\uparrow}f^{\dagger}_{j\downarrow}f_{j\downarrow}$