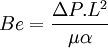To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bejan numberThere are two Bejan numbers (Be) in use, named after Duke University professor Adrian Bejan in two scientific domains: thermodynamics and fluid mechanics. Product highlight
ThermodynamicsIn the context of thermodynamics, the Bejan number is the ratio of heat transfer irreversibility to total irreversibility due to heat transfer and fluid friction: where
This definition was introduced by Paoletti et al. (see reference). Fluid mechanics and heat transferIn the context of fluid mechanics and heat transfer. the Bejan number is the dimensionless pressure drop along a channel of length L: where
The Be number plays in forced convection the same role that the Rayleigh number plays in natural convection. The Be number was introduced by Bhattacharjee and Grosshandler (see references) See also
References
Categories: Thermodynamics | Fluid dynamics | Convection |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bejan_number". A list of authors is available in Wikipedia. |





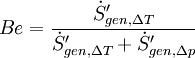
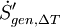 is the entropy generation contributed by heat transfer
is the entropy generation contributed by heat transfer
 is the entropy generation contributed by fluid friction.
is the entropy generation contributed by fluid friction.