To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Birch–Murnaghan equation of stateIn continuum mechanics, an equation of state suitable for modeling solids is naturally rather different from the ideal gas law. A solid has a certain equilibrium volume V0, and the energy increases quadratically as volume is increased or decreased a small amount from that value. The simplest plausible dependence of energy on volume would be a harmonic solid, with Product highlightThe next simplest reasonable model would be with a constant bulk modulus Murnaghan equation of stateA more sophisticated equation of state was derived by Francis D. Murnaghan of Johns Hopkins University in 1944. To begin with, we consider the pressure and the bulk modulus Experimentally, the bulk modulus pressure derivative is found to change little with pressure. If we take B' = B'0 to be a constant, then
where B0 is the value of B when P = 0. We may equate this with (2) and rearrange as Integrating this results in or equivalently Substituting (6) into Many substances have a fairly constant B'0 of about 3.5. Birch–Murnaghan equation of stateThe third-order Birch–Murnaghan isothermal equation of state, published in 1947 by Francis Birch of Harvard, is given by: Again, E(V) is found by integration of the pressure: References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Birch–Murnaghan_equation_of_state". A list of authors is available in Wikipedia. |


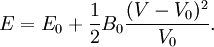



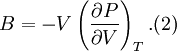
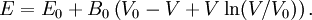
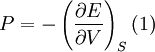
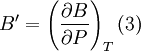
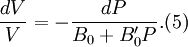
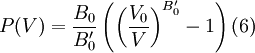
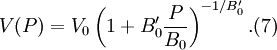
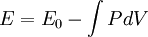 then results in the equation of state
for energy.
then results in the equation of state
for energy.
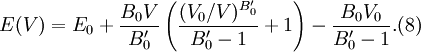
![P(V)=\frac{3B_0}{2} \left[\left(\frac{V_0}{V}\right)^\frac{7}{3} - \left(\frac{V_0}{V}\right)^\frac{5}{3}\right] \left\{1+\frac{3}{4}\left(B_0^\prime-4\right) \left[\left(\frac{V_0}{V}\right)^\frac{2}{3} - 1\right]\right\}](images/math/e/a/c/eac6109009a60ca850d784ae7b8783dd.png)
![E(V) = E_0 + \frac{9V_0B_0}{16} \left\{ \left[\left(\frac{V_0}{V}\right)^\frac{2}{3}-1\right]^3B_0^\prime + \left[\left(\frac{V_0}{V}\right)^\frac{2}{3}-1\right]^2 \left[6-4\left(\frac{V_0}{V}\right)^\frac{2}{3}\right]\right\}](images/math/9/c/6/9c68b3fd8a2ccf34b99e89fb629b6391.png)


