To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Born-von Karman boundary conditionThe Born-von Karman boundary condition is a set of boundary conditions which impose the restriction that a wave function must be periodic on a certain Bravais lattice. This condition is often applied in solid state physics to model an ideal crystal. Product highlightThe condition can be stated as
where i runs over the dimensions of the Bravais lattice, the ai are the primitive vectors of the lattice, and the Ni are any integers (assuming the lattice is infinite). This definition can be used to show that for any lattice translation vector T such that:
The Born-von Karman boundary condition is important in solid state physics for analyzing many features of crystals, such as diffraction and the band gap. Modeling the potential of a crystal as a periodic function with the Born-von Karman boundary condition and plugging in Schroedinger's equation results in a proof of Bloch's theorem, which is particularly important in understanding the band structure of crystals. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Born-von_Karman_boundary_condition". A list of authors is available in Wikipedia. |





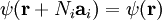 ,
,
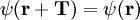
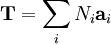 .
.


