To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Burgers' equationBurgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow. It is named for Johannes Martinus Burgers (1895-1981). Product highlightFor a given velocity u and viscosity coefficient ν, the general form of Burgers' equation is:
When ν = 0, Burgers' equation becomes the inviscid Burgers' equation:
which is a prototype for equations for which the solution can develop discontinuities (shock waves). SolutionThe inviscid Burgers' equation is a first order partial differential equation. Its solution can be constructed by the method of characteristics. This method yields that if X(t) is a solution of the ordinary differential equation then U(t): = u[X(t),t] is constant as a function of t. Hence [X(t),U(t)] is a solution of the system of ordinary equations The solutions of this system are given in terms of the initial values by Substitute X(0) = η, then U(0) = u[X(0),0] = u(η,0). Now the system becomes Conclusion: This is an implicit relation that determines the solution of the inviscid Burgers' equation. The viscous Burgers equation can be linearized by the Cole-Hopf substitution which turns it into the diffusion equation That allows one to solve an initial value problem: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Burgers'_equation". A list of authors is available in Wikipedia. |





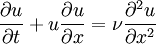 .
.
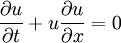 ,
,
![\frac{dX(t)}{dt} = u[X(t),t]](images/math/9/a/f/9afd1c418aa58e11158eaec5c485eb2b.png)
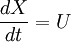
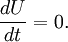
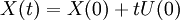
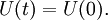
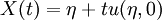
![\displaystyle u(\eta,0)=U(0)=U(t)=u[X(t),t]=u[\eta+tu(\eta,0),t].](images/math/d/6/3/d63727b1e411197082bda59c30159236.png)
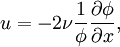
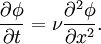
![u(x,t)=-2\nu\frac{\partial}{\partial x}\ln\Bigl\{(4\pi\nu t)^{-1/2}\int_{-\infty}^\infty\exp\Bigl[-\frac{(x-x')^2}{4\nu t} -\frac{1}{2\nu}\int_0^{x'}u(x'',0)dx''\Bigr]dx'\Bigr\}.](images/math/2/3/0/230eb0d52cda0cab7601378e9c3143a4.png)


