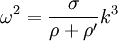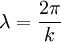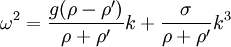To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Capillary wave
A capillary wave is a wave travelling along the interface between two fluids, whose dynamics are dominated by the effects of surface tension. Capillary waves are common in nature and the home and are often referred to as ripples. The wavelength of capillary waves is typically less than about a centimeter. Product highlightThe dispersion relation for capillary waves is where ω is the frequency, σ the surface tension, ρ the density of the
heavier fluid, ρ' the density of the lighter fluid and k the wavenumber. The wavelength is
The waves with large wavelengths are generally also affected by gravity and are then called gravity-capillary waves. Their dispersion relation reads, for infinite depth of the two fluids, where ω is the frequency, g the acceleration due to gravity, σ the surface tension, ρ the density and k the wavenumber. This class of waves involves ocean surface waves. In water on earth this is observed: Gravity waves have a group velocity half the phase velocity. Following a single wave in a group one can see the wave appearing at the back of the group, growing and finally disappearing at the front of the group. Therefore an interesting and common situation occurs when the dispersion caused by gravity cancels out the dispersion due to the capillary effect. At wavelength around 2 cm the capillary effect causes group velocity to equal phase velocity. The dispersion is zero, and a wave ridge can travel for long distances. Shorter (i.e. 2 mm) ripples do the opposite: the wave appears at the front of the group, growing and finally disappearing at the back of the group. See also |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Capillary_wave". A list of authors is available in Wikipedia. |