To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Capillary action
Capillary action, capillarity, capillary motion, or wicking is the ability of a substance to draw another substance into it. The standard reference is to a tube in plants but can be seen readily with porous paper. It occurs when the adhesive intermolecular forces between the liquid and a substance are stronger than the cohesive intermolecular forces inside the liquid. The effect causes a concave meniscus to form where the substance is touching a vertical surface. The same effect is what causes porous materials such as sponges to soak up liquids. A common apparatus used to demonstrate capillary action is the capillary tube. When the lower end of a vertical glass tube is placed in a liquid such as water, a concave meniscus forms. Surface tension pulls the liquid column up until there is a sufficient mass of liquid for gravitational forces to overcome the intermolecular forces. The weight of the liquid column is proportional to the square of the tube's diameter, but the contact length (around the edge) between the liquid and the tube is proportional only to the diameter of the tube, so a narrow tube will draw a liquid column higher than a wide tube. For example, a glass capillary tube 0.5 mm in diameter will lift a theoretical 2.8 cm column of water. Actual observations show shorter total distances. With some pairs of materials, such as mercury and glass, the interatomic forces within the liquid exceed those between the solid and the liquid, so a convex meniscus forms and capillary action works in reverse. Product highlight
ExamplesIn hydrology, capillary action describes the attraction of water molecules to soil particles. Capillary action is responsible for moving groundwater from wet areas of the soil to dry areas. Differences in soil matric potential (Ψm) drive capillary action in soil. Capillary action is also essential for the drainage of constantly produced tear fluid from the eye, two canalicula of tiny diameter are present in the inner corner of the eyelid, also called the lacrymal ducts; their openings can be seen with the naked eye within the lacrymal sacs when the eyelids are everted. Paper towels absorb liquid through capillary action, allowing a fluid to be transferred from a surface to the towel. The small pores of a sponge act as small capillaries, causing it to adsorb a comparatively large amount of fluid. Some modern sport and exercise fabrics, such as Coolmax, use capillary action to "wick" sweat away from the skin. These are often referred to as wicking fabrics, presumably after the capillary properties of a candle wick. Chemists utilize capillary action in thin layer chromatography, in which a solvent moves vertically up a plate via capillary action. Dissolved solutes travel with the solvent at various speeds depending on their polarity. FormulaWith notes on the dimension in SI units, the height h of a liquid column (m) is given by:[1] where:
For a water-filled glass tube in air at sea level, therefore, the height of the water column is given by:
Thus for a 2 m wide (1 m radius) tube, the water would rise an unnoticeable 0.014 mm. However, for a 2 cm wide tube, the water would rise 1.4 mm and for tube with radius 0.2 mm, the water would rise 14 cm (about 6 inches). MiscellaneousAlbert Einstein's first paper[2] submitted to Annalen der Physik was on capillarity. It was titled Folgerungen aus den Capillaritätserscheinungen, which translates as Conclusions from the capillarity phenomena, found in volume 4, page 513.[3] It was submitted in late 1900 and was published in 1901. In 1905 Einstein published four seminal papers in the same journal. See also
References |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Capillary_action". A list of authors is available in Wikipedia. |






 is the liquid-air
is the liquid-air 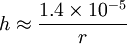 .
.


