To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Washburn's equationIn physics, Washburn's equation describes capillary flow in porous materials. Product highlightIt is where t is the time for a liquid of viscosity η and surface tension γ to penetrate a distance L into a fully wettable, porous material whose average pore diameter is D. The equation is derived for capillary flow in a cylindrical tube in the absence of a gravitational field, but according to physicist Len Fisher can be extremely accurate for more complex materials including biscuits (see dunk (biscuit)). Following National biscuit dunking day, some newspaper articles quoted the equation as Fisher's equation. In his paper from 1921 Washburn applies Poiseuille's law for fluid motion in a circular tube. Inserting the expression for the differential volume in terms of the length l of fluid in the tube dV = πr2dl, one obtains where
where ρ is the density of the liquid and γ its surface tension. ψ is the angle of the tube with respect to the horizontal axis. φ is the contact angle of the liquid on the capillary material. Substituting these expressions leads to the first-order differential equation for the distance the fluid penetrates into the tube l: The solutions of this differential equation are also discussed in this paper. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Washburn's_equation". A list of authors is available in Wikipedia. |
- Measurement times in materials analysis can be shortened - without loss of accuracy - This saves energy and opens up new potential for industrial applications
- Phorone
- Method Milestone for Quantum Physics: Rapid Test for Topological 2D Materials - This breakthrough could help accelerate the progress of this booming class of materials
- Indium_tin_oxide
- Diaphragm_compressor





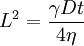
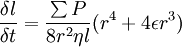
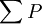 is the sum over the participating pressures, such as the atmospheric pressure
is the sum over the participating pressures, such as the atmospheric pressure 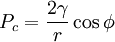
}{8 r^2 \eta l}](images/math/8/7/c/87ca2c223f4d1b6d2a7eca0869ddef25.png)


