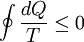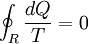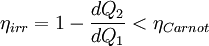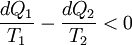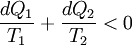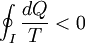Clausius theorem

Clausius theorem (1854) states that in a cyclic process

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

How to quickly check pipettes?

Guide to balance cleaning: 8 simple steps

The equality holds in the reversible case and the '<' is in the irreversible case. The reversible case is used to introduce the function state entropy. This is because in cyclic process the variation of a state function is zero.

First we have to prove the lemma: "any reversible process can be replaced by a combination of reversible isothermal and adiabatic processes".

Consider a reversible process a-b. A series of isothermal and adiabatic processes can replace this process if the heat and work interaction in those processes is the same as that in the process a-b. Let this process be replaced by the process a-c-d-b, where a-c and d-b are reversible adiabatic processes, while c-d is a reversible isothermal process. The isothermal line is chosen such that the area a-e-c is the same as the area b-e-d. Now, since the area under the p-V diagram is the work done for a reversible process, we have, the total work done in the cycle a-c-d-b-a is zero. Applying the first law, we have, the total heat transferred is also zero as the process is a cycle. Since a-c and d-b are adiabatic processes, the heat transferred in process c-d is the same as that in the process a-b. Now applying first law between the states a and b along a-b and a-c-d-b, we have, the work done is the same. Thus the heat and work in the process a-b and a-c-d-b are the same and any reversible process a-b can be replaced with a combination of isothermal and adiabatic processes, which is the Clausius theorem.

A corollary of this theorem is that any reversible cycle can be replaced by a series of Carnot cycles.

Suppose each of these Carnot cycles absorbs heat dQ₁ⁱ at temperature T₁ⁱ and rejects heat dQ₂ⁱ at T₂ⁱ. Then, for each of these engines, we have dQ₁ⁱ/dQ₂ⁱ = −T₁ⁱ/T₂ⁱ (i.e. dQ₁ⁱ/T₁ⁱ + dQ₂ⁱ/T₂ⁱ = 0). The negative sign is included as the heat lost from the body has a negative value. Summing over a large number of these cycles, we have, in the limit,

This means that the quantity dQ/T is a property. It is given the name entropy.

Further, using Carnot's principle, for an irreversible cycle, the efficiency is less than that for the Carnot cycle, so that

As the heat is transferred out of the system in the second process, we have, assuming the normal conventions for heat transfer,

So that, in the limit we have,

The above inequality is called the inequality of Clausius. Here the equality holds in the reversible case.