To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Conditional quantum entropyThe conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory. The conditional entropy is written S(ρ | σ), or H(ρ | σ), depending on the notation being used for the von Neumann entropy. Product highlightFor the remainder of the article, we use the notation S(ρ) for the von Neumann entropy. DefinitionGiven two quantum states ρ and σ, the von Neumann entropies are S(ρ) and S(σ). The von Neumann entropy measures how uncertain we are about the value of the state; how much the state is a mixed state. The joint quantum entropy S(ρ,σ) measures our uncertainty about the joint system which contains both states. By analogy with the classical conditional entropy, one defines the conditional quantum entropy as An equivalent (and more intuitive) operational definition of the quantum conditional entropy (as a measure of the quantum communication cost or surplus when performing quantum state merging) was given by Michał Horodecki, Jonathan Oppenheim, and Andreas Winter in their paper "Quantum Information can be negative" [1]. PropertiesUnlike the classical conditional entropy, the conditional quantum entropy can be negative. ReferencesNielsen, Michael A. and Isaac L. Chuang (2000). Quantum Computation and Quantum Information. Cambridge University Press, ISBN 0-521-63503-9. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Conditional_quantum_entropy". A list of authors is available in Wikipedia. |





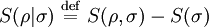 .
.


