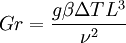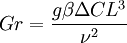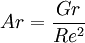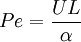Convective heat transfer

Convective heat transfer is a mechanism of heat transfer occurring because of bulk motion (observable movement) of fluids. This can be contrasted with conductive heat transfer, which is the transfer of energy molecule by molecule through a solid or fluid, and radiative heat transfer, the transfer of energy through electromagnetic waves.

Additional recommended knowledge

Correct Test Weight Handling Guide: 12 Practical Tips

Safe Weighing Range Ensures Accurate Results

Daily Visual Balance Check

Convective heat transfer is split into two categories: natural (or free) convection and forced (or advective) convection, also known as heat advection.

Natural convective heat transfer

Natural convection is a mechanism, or type of heat transport in which the fluid motion is not generated by any external source (like a pump, fan, suction device, etc.) but only by density differences in the fluid occurring due to temperature gradients. In natural convection, fluid surrounding a heat source receives heat, becomes less dense and rises. The surrounding, cooler fluid then moves to replace it. This cooler fluid is then heated and the process continues, forming a convection current. The driving force for natural convection is buoyancy, a result of differences in fluid density. Because of this, the presence of gravity or an equivalent force (arising from the equivalence principle, such as acceleration, centrifugal force or Coriolis force) is essential for natural convection. Natural convection does not operate as it does on Earth in the micro gravity environment of the orbiting International Space Station, where other heat transfer mechanisms are required to prevent electronic components from overheating.

Natural convection has attracted a great deal of attention by researchers because of its presence both in nature, seen in the rising plume of hot air from fire, oceanic currents, and sea-wind formation, and in engineering applications like formation of microstructures during the cooling of molten metals and in shrouded fins and solar ponds. Mathematically, the tendency of a particular system towards natural convection relies on the Grashof number (Gr), which is a ratio of buoyancy force and viscous force.^[1]

$Gr= \frac{g \beta \Delta T L^3}{\nu^2}$

The parameter $β$ is the rate of change of density with respect to the change in temperature (T), and ν is the viscosity. Thus, the Grashof number can be thought of as the ratio of the upwards buoyancy of the heated fluid to the internal friction slowing it down. In very sticky, viscous fluids, fluid movement is restricted, along with natural convection. In the extreme case of infinite viscosity, the fluid could not move and all heat transfer would be through conductive heat transfer.

A similar equation can be written for natural convection occurring due to a concentration gradient, sometimes termed thermo-solutal convection. In this case, a concentration of hot fluid diffuses into a cold fluid, in much the same way that ink poured into a container of water diffuses to dye the entire space.

$Gr= \frac{g \beta \Delta C L^3}{\nu^2}$

Forced convective heat transfer (advective heat transfer)

Forced convection is a mechanism, or type of heat transport in which fluid motion is generated by an external source (like a pump, fan, suction device, etc.). Forced convection is often encountered by engineers designing or analyzing heat exchangers, pipe flow, and flow over a plate at a different temperature than the stream (the case of a shuttle wing during re-entry, for example). However, in any forced convection situation, some amount of natural convection is always present. When the natural convection is not negligible, such flows are typically referred to as mixed convection.

When analysing potentially mixed convection, a parameter called the Archimedes number (Ar) parametizes the relative strength of free and forced convection. The Archimedes number is the ratio of Grashof number and the square of Reynolds number, which represents the ratio of buoyancy force and inertia force, and which stands in for the contribution of natural convection. When Ar >> 1, natural convection dominates and when Ar << 1, forced convection dominates.

$Ar= \frac{Gr}{Re^2}$ ^[2]

When natural convection isn't a significant factor, mathematical analysis with forced convection theories typically yields accurate results. The parameter of importance in forced convection is the Peclet number, which is the ratio of advection (movement by currents) and diffusion (movement from high to low concentrations) of heat.

$Pe=\frac{U L}{\alpha }$

When the Peclet number is much greater than unity (1), advection dominates diffusion. Similarly, much smaller ratios indicate a higher rate of diffusion relative to advection.

Textbooks / Reference Books

^ Kays, William; Crawford, Michael; Weigand, Bernhard (2004). Convective Heat and Mass Transfer, 4E. McGraw-Hill Professional. ISBN 0072990732.
^ Incropera, F. (2001). Fundamentals of Heat and Mass Transfer, 5th Ed.. Wiley. ISBN-13 978-0471386506.

Cebeci, Tuncer (2002). Convective Heat Transfer. Springer. ISBN 096684615X.

Burmeister, Louis (1993). Convective Heat Transfer, 2E. Wiley-Interscience. ISBN 047157709X.

Categories: Heat | Thermodynamics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Convective_heat_transfer". A list of authors is available in Wikipedia.