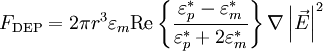To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
DielectrophoresisDielectrophoresis (or DEP) is a phenomenon in which a force is exerted on a dielectric particle when it is subjected to a non-uniform electric field. This force does not require the particle to be charged. All particles exhibit dielectrophoretic activity in the presence of electric fields. However, the strength of the force depends strongly on the medium and particles' electrical properties, on the particles' shape and size, as well as on the frequency of the electric field. Consequently, fields of a particular frequency can manipulate particles with great selectivity. This has allowed, for example, the separation of cells or the orientation and manipulation of nanoparticles and nanowires.
Product highlight
Background and PropertiesPublications on dielectrophoresis go as far back as the 1950's, by Herbert Pohl[1][2]. Recently, dielectrophoresis has been revived due to its potential in the manipulation of microparticles, nanoparticles and cells. Pohl wrote in his book[3] defining dielectrophoresis as the translational motion of neutral matter caused by polarization effects in a nonuniform electric field. The phenomenological bases are catalogued below:
Phenomena associated with dielectrophoresis are electrorotation and traveling wave dielectrophoresis (TWDEP). Dielectrophoresis can be enhanced using multiple frequencies, in what is known as multiple-frequency dielectrophoresis (MFDEP).
Dielectrophoretic forceFor a field-aligned prolate ellipsoid of radius r and length l (r > l) with complex dielectric constant The complex dielectric constant is This equation is accurate for highly elongated ellipsoids when the electric field gradients are not very large (e.g., close to electrode edges). The equation only takes into account the dipole formed and not higher order polarisation. When the electric field gradients are large, higher order terms become relevant, and result in higher forces. To be precise, the time-dependent equation only applies to lossless particles, because loss creates a lag between the field and the induced dipole. When averaged, the effect cancels out and the equation holds true for lossy particles as well. An equivalent time-averaged equation can be easily obtained by replacing E with Erms, or, for sinusoidal voltages by dividing the right hand side by 2. For a homogeneous sphere of radius r and complex permittivity The factor in parentheses is known as the complex Clausius-Mossotti function and contains all the frequency dependence of the DEP force. Once again, a time-averaged force can be achieved by using Erms.
Dielectrophoresis Field-Flow Fractionation (DEP-FFF)The utilization of the difference between dielectrophoretic forces exerted on different particles in nonuniform electric fields is known as DEP separation. The exploitation of DEP forces has been classified into two groups: DEP migration and DEP retention. DEP migration uses DEP forces that exert opposite signs of force on different particle types to attract some of the particles and repel others[5]. DEP retention uses the balance between DEP and fluid-flow forces. Particles experiencing repulsive and weak attractive DEP forces are eluted by fluid flow, whereas particles experiencing strong attractive DEP forces are trapped at electrode edges against flow drag[6]. Dielectrophoresis Field-Flow Fractionation, introduced by Davis and Giddings[7], is a family of chromatographic-like separation methods. In DEP-FFF, DEP forces are combined with drag flow to fractionate a sample of different types of particles[6][8][9][10]. Particles are injected into a carrier flow that passes through the separation chamber, with an external separating force (a DEP force) being applied perpendicular to the flow. By means of different factors, such as diffusion and steric, hydrodynamic, dielectric and other effects, or a combination thereof, particles (<1 μm in diameter) with different dielectric or diffusive properties attain different positions away from the chamber wall, which, in turn, exhibit different characteristic concentration profile. Particles that move further away from the wall reach higher positions in the parabolic velocity profile of the liquid flowing through the chamber and will be eluted from the chamber at a faster rate.
References
Categories: Electrophoresis | Analytical chemistry | Nanotechnology | Colloidal chemistry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Dielectrophoresis". A list of authors is available in Wikipedia. |





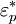 in a medium with complex dielectric constant
in a medium with complex dielectric constant 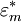 the time-dependent dielectrophoretic force is given by
the time-dependent dielectrophoretic force is given by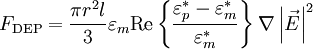
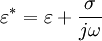 , where
, where