To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Disk laserA disk laser or active mirror (Fig.1.) is a type of solid-state laser characterized by a heat sink and laser output that are realized on opposite sides of a thin layer of active gain medium.[1] Despite their name, disk lasers do not have to be circular; other shapes have also been tried. Disk lasers should not be confused with Laserdiscs, which are a disk-shaped optical storage medium. Disk lasers should not be confused with Fiber laser disks, which are a disk-shaped coils of a fiber lasers, pumped from side. Product highlight
Active mirrors and disk lasersInitially, disk lasers were called active mirrors, because the gain medium of a disk laser is essentially an optical mirror with reflection coefficient greater than unity. An active mirror is a thin disk-shaped double-pass optical amplifier. The first active mirrors were developed in the Laboratory for Laser Energetics (USA) [3] and the Institute for Laser Science (Japan) [2]. Then, the concept was developed in various research groups, in particular, the University of Stuttgart (Germany)[4] and Tokyo Institute of Technology (Japan) [5] for Yb:doped glasses and semiconductor laser materials. In the disk laser, the heat sink does not have to be transparent, so, it can be extremely efficient even at large transverse size Limit of power scaling for disk lasersThe power of such lasers is limited not only by the power of pump available, but also by overheating, amplified spontaneous emission (ASE) and
the background round-trip loss.[6]
To avoid overheating, the size Some features of the power scaling can revealed from a simple model.
Let An additional issue is the efficient delivery of pump. At the low round-trip gain, the single-pass absorption of pump is also low. Therefore, the recycling of pump is required for the efficient operation. (See the additional mirror M at the left-hands side of figure 2.) For the power scaling, the medium should be optically thin, and many passes of pump required; the lateral delivery of pump [7] also might be a possible solution. Anti-ASE capIn order to reduce the impact of ASE, an anti-ASE cap consisting of undoped material on the surface of a disk laser has been suggested[8]. Such a cap allows spontaneously emitted photons to escape from the active layer and prevents them from resonating in the cavity. This could allow an order of magnitude increase in the maximum power achievable by a disk laser[9]. See alsoReferences
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Disk_laser". A list of authors is available in Wikipedia. |





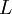 of the device (Fig.1.).
The increase in size may allow the
of the device (Fig.1.).
The increase in size may allow the 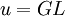 cannot be large.
This requires to reduce the gain
cannot be large.
This requires to reduce the gain 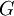 ;
this gain is determined by the reflectivity of the output coupler and thickness
;
this gain is determined by the reflectivity of the output coupler and thickness 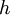 .
The
.
The 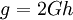 should remain larger than the
round-trip loss
should remain larger than the
round-trip loss 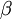 (the difference
(the difference 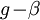 determines the part of the energy of the optical field,
which can be outputed from the laser cavity at each round-trip).
The reduction of gain
determines the part of the energy of the optical field,
which can be outputed from the laser cavity at each round-trip).
The reduction of gain 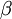 ,
requires to increase the thickness
,
requires to increase the thickness 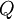 be the
be the 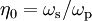 be the ratio of frequencies,
be the ratio of frequencies,
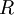 be the thermal loading parameter.
The key parameter
be the thermal loading parameter.
The key parameter
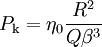 determines the maximal power of the disk laser.
The correspnding optimal thickness can be estimated with
determines the maximal power of the disk laser.
The correspnding optimal thickness can be estimated with
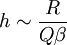 .
The corresponding optimal size
.
The corresponding optimal size
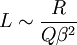 .
Roughly, the round-trip loss should scale inversely proportionally to cubic root of the power required.
.
Roughly, the round-trip loss should scale inversely proportionally to cubic root of the power required.


