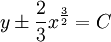My watch list

Euler-Tricomi equation

In mathematics, the Euler-Tricomi equation is a linear partial differential equation useful in the study of transonic flow. It is named for Leonhard Euler and Francesco Giacomo Tricomi.

u x x = x u y y .

Additional recommended knowledge

What is the Sensitivity of my Balance?

Don't let static charges disrupt your weighing accuracy

Essential Laboratory Skills Guide

It is hyperbolic in the half plane $x > 0$ and elliptic in the half plane $x < 0$ . Its characteristics are $x d x 2 = d y 2$ , which have the integral

$y\pm\frac{2}{3}x^{\frac{3}{2}}=C$

where $C$ is a constant of integration. The characteristics thus comprise two families of semicubical parabolas, with cusps on the line $x = 0$ , the curves lying on the right hand side of the y-axis.

Particular solutions

Particular solutions to the Euler-Tricomi equations include

$u = A x y + B x + C y + D$
$u = A (3 y 2 + x 3) + B (y 3 + x 3 y) + C (6 x y 2 + x 4)$

where $A, B, C, D$ are arbitrary constants.

The Euler-Tricomi equation is a limiting form of Chaplygin's equation.

Bibliography

A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, 2002.

Category: Equations of fluid dynamics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Euler-Tricomi_equation". A list of authors is available in Wikipedia.

The LUMITOS industry portals