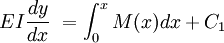Flexural rigidity

Flexural rigidity is defined as the force couple required to bend a rigid structure to a unit curvature.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

Safe Weighing Range Ensures Accurate Results

Daily Sensitivity Test

In a beam or rod, flexural rigidity varies along the length as a function of x shown in the following equation:

where E is the modulus of elasticity, I is the 2nd moment of inertia, y is the transverse displacement of the beam at x, and M(x) is the bending moment at x.

Flexural rigidity has SI units of Pa·m⁴ (which also equals N·m²).

Flexure of the lithosphere

The thin lithospheric plates which cover the surface of the Earth are also subject to flexure, when a load or force is applied to them. On a geological timescale, the lithosphere behaves elastically and can therefore bend under loading by mountain chains, volcanoes and so on.

The flexure of the plate depends on:

1. The plate thickness
2. The elastic properties of the plate
3. The applied load or force

As flexural rigidity of the plate is determined by the Young's modulus, Poisson's ratio and cube of the plate thickness, it is a governing factor in both (1) and (2).

See also

• Euler-Bernoulli beam equation