To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Marcus theory
Marcus Theory is a theory originally developed by Rudolph A. Marcus to explain outer sphere electron transfer, the transfer of electrons between two metal spheres, by introducing reorganization energy and electronic coupling to the reaction coordinate diagram typically portraying the Gibbs' Free Energy and thermodynamic transition state. The theory was also later extended to inner sphere electron transfer by Noel Hush. The resultant theory, called Marcus-Hush theory, will also be discussed here. Besides the inner and outersphere applications, Marcus theory has been extended to address heterogeneous electron transfer. Product highlightRudolph Marcus received the Nobel Prize in Chemistry in 1992 for this theory. Marcus theory is used in various aspects of chemistry and biology, including photosynthesis, corrosion, certain types of chemiluminescence and more. Marcus theory is currently the dominant theory of electron transfer in chemistry. Marcus theory is so widely accepted because it makes several predictions concerning electron transfer that have been proven true over the last several decades. The most salient points of the theory are;
The basic equation of Marcus theory is:
where ket is the rate of electron transfer, The key parameters are diagrammed here:
The left hand parabola represents the Potential energy surface for the nuclear motion of the reactants in the initial state (where the electron is still on the donor molecule or group}, and the right hand parabola represents the potential energy surface for the nuclear motion of the products in the final state (after the electron has transferred from the donor to the acceptor). The unusual dependence of the electron transfer rate on the free energy change (i.e., the
Additional information
Marcus's Key PapersMarcus, R.A. J. Chem. Phys. 1956, 24, 966. Marcus, R.A. J. Chem. Phys. 1956, 24, 979. Marcus, R.A. J. Chem. Phys. 1957, 26, 867. Marcus, R.A. J. Chem. Phys. 1957, 26, 872. Marcus, R.A. Disc. Faraday Soc. 1960, 29, 21. Marcus, R.A. J. Phys. Chem. 1963, 67, 853. Marcus, R.A. Annu. Rev. Phys. Chem. 1964, 15, 155. Marcus, R.A. J. Chem. Phys. 1965, 43, 679. Marcus, R.A.; Sutin N. Biochem. Biophys. Acta 1985, 811, 265. References
|
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Marcus_theory". A list of authors is available in Wikipedia. |





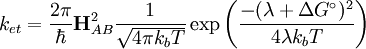
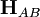 is the electronic coupling between the initial and final states,
is the electronic coupling between the initial and final states, 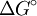 is the total
is the total 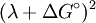 term in the equation), which leads to the Marcus inverted region, follows simply from assuming that the potential energy of the initial and final states varies quadratically with some reaction coordinate (i.e. that both potential energy surfaces are parabolas), solving for the activation energy in terms of
term in the equation), which leads to the Marcus inverted region, follows simply from assuming that the potential energy of the initial and final states varies quadratically with some reaction coordinate (i.e. that both potential energy surfaces are parabolas), solving for the activation energy in terms of 

