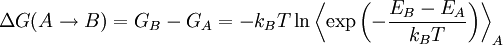Free energy perturbation

Free energy perturbation (FEP) theory is a method based on statistical mechanics that is used in computational chemistry for computing free energy differences from molecular dynamics or Metropolis Monte Carlo simulations. The FEP method was introduced by R. W. Zwanzig in 1954.^[1] According to free-energy perturbation theory, the free energy difference for going from state A to state B is obtained from the following equation, known as the Zwanzig equation:

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Daily Sensitivity Test

Correct Test Weight Handling Guide: 12 Practical Tips

where T is the temperature, k_B is Boltzmann's constant, and the triangular brackets denote an average over a simulation run for state A. In practice, one runs a normal simulation for state A, but each time a new configuration is accepted, the energy for state B is also computed. The difference between states A and B may be in the atom types involved, in which case the ΔG obtained is for "mutating" one molecule onto another, or it may be a difference of geometry, in which case one obtains a free energy map along one or more reaction coordinates. This free energy map is also known as a potential of mean force or PMF. Free energy perturbation calculations only converge properly when the difference between the two states is small enough; therefore it is usually necessary to divide a perturbation into a series of smaller “windows”, which are computed independently. Since there is no need for constant communication between the simulation for one window and the next, the process can be trivially parallelized by running each window in a different CPU, in what is known as an “embarrassingly parallel” setup.

FEP calculations have been used for studying host-guest binding energetics, pKa predictions, solvent effects on reactions, and enzymatic reactions. For the study of reactions it is often necessary to involve a quantum-mechanical representation of the reaction center because the molecular mechanics force fields used for FEP simulations can't handle breaking bonds. A hybrid method that has the advantages of both QM and MM calculations is called QM/MM.

References

1. ^ Zwanzig, R. W. J. Chem. Phys. 1954, 22, 1420-1426. doi:10.1063/1.1740409