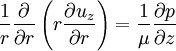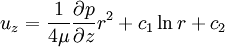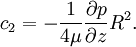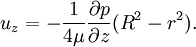To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hagen-Poiseuille flowThe flow of fluid through a pipe of uniform (circular) cross-section is known as Hagen-Poiseuille flow. The Hagen-Poiseuille flow is an exact solution of the Navier-Stokes equations in fluid mechanics. The equations governing the Hagen-Poiseuille flow can be derived from the Navier-Stokes equation in cylindrical coordinates by making the following set of assumptions:
Product highlight
Since uz needs to be finite at r = 0, c1 = 0. The no slip boundary condition at the pipe wall requires that uz = 0 at r = R (radius of the pipe), which yields Thus we have finally the following parabolic velocity profile: The maximum velocity occurs at the pipe centerline (r=0): The average velocity can be obtained by integrating over the pipe cross-section: Internal Links: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hagen-Poiseuille_flow". A list of authors is available in Wikipedia. |


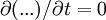 ).
).
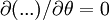 ) and fully developed (
) and fully developed (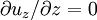 ).
).



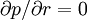 , i.e., the pressure
, i.e., the pressure