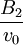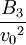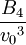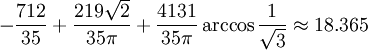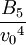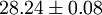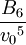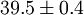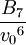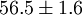To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hard spheresHard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong repulsion that atoms and spherical molecules experience at very close distances. Product highlightFormal definitionHard spheres of diameter σ are particles with the following pairwise interaction potential: where Virial coefficientsThe first three virial coefficients for hard spheres can be determined analytically
Higher-order ones can be determined numerically using Monte Carlo integration. We list
Literature
|
||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hard_spheres". A list of authors is available in Wikipedia. |





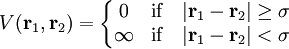
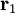 and
and 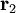 are the positions of the two particles.
are the positions of the two particles.