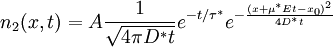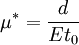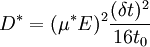To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Haynes - Shockley experimentIn the Haynes - Shockley experiment, a piece of semiconductor gets a pulse of holes, induced by voltage or a short laser pulse. Product highlightTo see the effect, we consider a n-type semiconductor with the length d. We are interested in determining the mobility of the carriers, diffusion constant and relaxation time. In the following, we reduce the problem to one dimension. The equations for electron and hole currents are: where μ = eβD is mobility, Einstein relation states: v = μE. We consider the continuity equation: The electrons and the holes recombine with the time τ. We define p1 = p − p0 and n1 = n − n0 so the upper equations can be rewritten as: Let us consider the part with the gradient of the electric field. Laplace equation states: Introducing n2 = p1 + n1 and n3 = p1 − n1 < < n2, we rewrite the initial equations with the new parameters. These two equations are coupled and can be combined: kjer so Considering n>>p or The final equation for the carriers is: This can be interpreted as a delta function that is created immediately after the pulse. Holes then start to travel towards the electrode where we detect them. The signal then is Gaussian curve shaped. Parameters μ,D and τ can be obtained from the shape of the signal. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Haynes_-_Shockley_experiment". A list of authors is available in Wikipedia. |





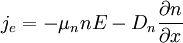
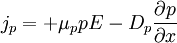
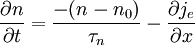
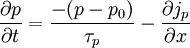
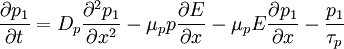
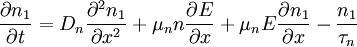
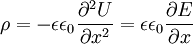
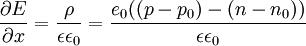
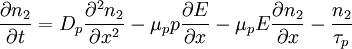
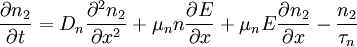
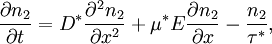
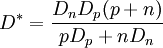 ,
, 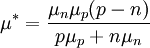 in
in
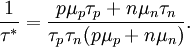
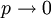 (that is a fair approximation for a semiconductor with only few holes injected), we see that
(that is a fair approximation for a semiconductor with only few holes injected), we see that  ,
,  and
and 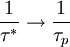 . The semiconductor behaves as if there were only holes traveling in it.
. The semiconductor behaves as if there were only holes traveling in it.