To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Henri Poincaré
Jules Henri Poincaré (April 29, 1854 – July 17, 1912) (IPA: [pwɛ̃kaʀe][1]) was one of France's greatest mathematicians and theoretical physicists, and a philosopher of science. Poincaré is often described as a polymath, and in mathematics as The Last Universalist, since he excelled in all fields of the discipline as it existed during his lifetime. As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. He was responsible for formulating the Poincaré conjecture, one of the most famous problems in mathematics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is considered to be one of the founders of the field of topology. Poincaré introduced the modern principle of relativity and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to Lorentz in 1905. Thus he obtained perfect invariance of all of Maxwell's equations, the final step in the formulation of the theory of special relativity. The Poincaré group used in physics and mathematics was named after him. Product highlight
LifePoincaré was born on April 29, 1854 in Cité Ducale neighborhood, Nancy, France into an influential family (Belliver, 1956). His father Leon Poincaré (1828-1892) was a professor of medicine at the University of Nancy (Sagaret, 1911). His adored younger sister Aline married the spiritual philosopher Emile Boutroux. Another notable member of Jules' family was his cousin, Raymond, who would become the President of France, 1913 to 1920, and a fellow member of the Académie française.[2] EducationDuring his childhood he was seriously ill for a time with diphtheria and received special instruction from his gifted mother, Eugénie Launois (1830-1897). In 1862 Henri entered the Lycée in Nancy (now renamed the Lycée Henri Poincaré in his honour, along with the University of Nancy). He spent eleven years at the Lycée and during this time he proved to be one of the top students in every topic he studied. He excelled in written composition. His mathematics teacher described him as a "monster of mathematics" and he won first prizes in the concours général, a competition between the top pupils from all the Lycées across France. (His poorest subjects were music and physical education, where he was described as "average at best" (O'Connor et al., 2002). However, poor eyesight and a tendency towards absentmindedness may explain these difficulties (Carl, 1968). He graduated from the Lycée in 1871 with a Bachelor's degree in letters and sciences. During the Franco-Prussian War of 1870 he served alongside his father in the Ambulance Corps. Poincaré entered the École Polytechnique in 1873. There he studied mathematics as a student of Charles Hermite, continuing to excel and publishing his first paper (Démonstration nouvelle des propriétés de l'indicatrice d'une surface) in 1874. He graduated in 1875 or 1876. He went on to study at the École des Mines, continuing to study mathematics in addition to the mining engineering syllabus and received the degree of ordinary engineer in March 1879. As a graduate of the École des Mines he joined the Corps des Mines as an inspector for the Vesoul region in northeast France. He was on the scene of a mining disaster at Magny in August 1879 in which 18 miners died. He carried out the official investigation into the accident in a characteristically thorough and humane way. At the same time, Poincaré was preparing for his doctorate in sciences in mathematics under the supervision of Charles Hermite. His doctoral thesis was in the field of differential equations. Poincaré devised a new way of studying the properties of these equations. He not only faced the question of determining the integral of such equations, but also was the first person to study their general geometric properties. He realised that they could be used to model the behaviour of multiple bodies in free motion within the solar system. Poincaré graduated from the University of Paris in 1879.
CareerSoon after, he was offered a post as junior lecturer in mathematics at Caen University, but he never fully abandoned his mining career to mathematics. He worked at the Ministry of Public Services as an engineer in charge of northern railway development from 1881 to 1885. He eventually became chief engineer of the Corps de Mines in 1893 and inspector general in 1910. Beginning in 1881 and for the rest of his career, he taught at the University of Paris (the Sorbonne). He was initially appointed as the maître de conférences d'analyse (associate professor of analysis) (Sageret, 1911). Eventually, he held the chairs of Physical and Experimental Mechanics, Mathematical Physics and Theory of Probability, and Celestial Mechanics and Astronomy. Also in that same year, Poincaré married Miss Poulain d'Andecy. Together they had four children: Jeanne (born 1887), Yvonne (born 1889), Henriette (born 1891), and Léon (born 1893). In 1887, at the young age of 32, Poincaré was elected to the French Academy of Sciences. He became its president in 1906, and was elected to the Académie française in 1909. In 1887 he won Oscar II, King of Sweden's mathematical competition for a resolution of the three-body problem concerning the free motion of multiple orbiting bodies. (See #The three-body problem section below) In 1893 Poincaré joined the French Bureau des Longitudes, which engaged him in the synchronisation of time around the world. In 1897 Poincaré backed an unsuccessful proposal for the decimalisation of circular measure, and hence time and longitude (see Galison 2003). It was this post which led him to consider the question of establishing international time zones and the synchronisation of time between bodies in relative motion. (See #Work on Relativity section below) In 1899, and again more successfully in 1904, he intervened in the trials of Alfred Dreyfus. He attacked the spurious scientific claims of some of the evidence brought against Dreyfus, who was a Jewish officer in the French army charged with treason by anti-Semitic colleagues. In 1912 Poincaré underwent surgery for a prostate problem and subsequently died from an embolism on July 17, 1912, in Paris. He was aged 58. He is buried in the Poincaré family vault in the Cemetery of Montparnasse, Paris. The French Minister of Education, Claude Allegre, has recently (2004) proposed that Poincaré be reburied in the Panthéon in Paris, which is reserved for French citizens only of the highest honour.[3] WorkPoincaré made many contributions to different fields of pure and applied mathematics such as: celestial mechanics, fluid mechanics, optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, quantum theory, theory of relativity and physical cosmology. He was also a populariser of mathematics and physics and wrote several books for the lay public. Among the specific topics he contributed to are the following:
The three-body problemThe problem of finding the general solution to the motion of more than two orbiting bodies in the solar system had eluded mathematicians since Newton's time. This was known originally as the three-body problem and later the n-body problem, where n is any number of more than two orbiting bodies. The n-body solution was considered very important and challenging at the close of the nineteenth century. Indeed in 1887, in honour of his 60th birthday, Oscar II, King of Sweden, advised by Gösta Mittag-Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:
In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. One of the judges, the distinguished Karl Weierstrass, said, "This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics." (The first version of his contribution even contained a serious error; for details see the article by Diacu). The version finally printed contained many important ideas which lead to the theory of chaos. The problem as stated originally was finally solved by Karl F. Sundman for n = 3 in 1912 and was generalised to the case of n > 3 bodies by Qiudong Wang in the 1990s. Work on relativityLocal timePoincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "luminiferous aether"), could be synchronised. At the same time Dutch theorist Hendrik Lorentz was developing Maxwell's theory into a theory of the motion of charged particles ("electrons" or "ions"), and their interaction with radiation. He had introduced the concept of local time and was using it to explain the failure of optical and electrical experiments to detect motion relative to the aether (see Michelson-Morley experiment). Poincaré (1900) discussed Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.[4] In "The Measure of Time" (Poincaré 1898), he discussed the difficulty of establishing simultaneity at a distance and concluded it can be established by convention. He also discussed the "postulate of the speed of light", and formulated the principle of relativity, according to which no mechanical or electromagnetic experiment can discriminate between a state of uniform motion and a state of rest. Thereafter, Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher, was interested in the "deeper meaning". Thus he interpreted Lorentz's theory in terms of the principle of relativity and in so doing he came up with many insights that are now associated with special relativity. Inertia of energyIn 1900 Henri Poincaré studied the conflict between the action/reaction principle and Lorentz ether theory. He tried to determine whether the center of gravity still moves with a uniform velocity when electromagnetic fields are included. He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. The electromagnetic field energy behaves like a fictitious fluid ("fluide fictif") with a mass density of E/c² and velocity c. If the center of mass frame is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible--it's neither created or destroyed--- then the motion of the center of mass frame remains uniform. But electromagnetic energy can be converted into other forms of energy. So Poincaré assumed that there exists a non-electric energy fluid at each point of space, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the center of mass remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions.[5] But Poincare's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a recoil from the inertia of the fictitious fluid. In the framework of Lorentz ether theory Poincare performed a Lorentz boost to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow a perpetuum mobile, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Poincaré came back to this topic in "Science and Hypothesis" (1902) and "The Value of Science" (1905). This time he rejected the possibility that energy carries mass: "... [the recoil] is contrary to the principle of Newton since our projectile here has no mass, it is not matter, it is energy". He also discussed two other unexplained effects: (1) non-conservation of mass implied by Lorentz's variable mass γm, Abraham's theory of variable mass and Kaufmann's experiments on the mass of fast moving electrons and (2) the non-conservation of energy in the radium experiments of Madame Curie. It was Einstein's insight that a body losing energy as radiation or heat was losing mass of amount m = E / c2 that resolved Poincare's paradox. The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame[6]. Einstein noted in 1906 that Poincaré's solution to the center of mass problem and his own were mathematically equivalent.[7] Lorentz transformationIn 1905 Poincaré wrote to Lorentz[8] about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance." In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge-occupied space, and also questioned the time dilation factor given by Lorentz. In a second letter to Lorentz,[9] Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all: it was necessary to make the Lorentz transformation form a group and gave what is now known as the relativistic velocity-addition law. Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that short paper he wrote
and showed that the arbitrary function Einstein's first paper on relativity was published three months after Poincaré's short paper, but before Poincaré's longer version. It relied on the principle of relativity to derive the Lorentz transformations and used the same clock synchronisation procedure that Poincaré (1900) had described, but was remarkable in that it contained no references at all. Poincaré never acknowledged Einstein's work on Special Relativity. Einstein acknowledged Poincaré in the text of a lecture in 1921 called Geometrie und Erfahrung in connection with the Non-Euclidean geometry, but not in connection with special relativity. A few years before his death Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognised that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ..." [10] AssessmentsPoincaré's work in the development of special relativity is well recognised (e.g. Darrigol 2004), though most historians stress that despite many similarities with Einstein's work, the two had very different research agendas and interpretations of the work (see Galison 2003 and Kragh 1999). A minority go much further, such as the historian of science Sir Edmund Whittaker, who held that Poincaré and Lorentz were the true discoverers of Relativity (Whittaker 1953). Poincaré consistently credited Lorentz's achievements, ranking his own contributions as minor. Thus, he wrote: "Lorentz has tried to modify his hypothesis so as to make it in accord with the postulate of complete impossibility of measuring absolute motion. He has succeeded in doing so in his article [Lorentz 1904]. The importance of the problem has made me take up the question again; the results that I have obtained agreement on all important points with those of Lorentz; I have been led only to modify or complete them on some points of detail." (Poincaré 1905) [emphasis added]. In an address in 1909 on "The New Mechanics", Poincaré discussed the demolition of Newton's mechanics brought about by Max Abraham and Lorentz, without mentioning Einstein. In one of his last essays entitled "The Quantum Theory" (1913), when referring to the Solvay Conference, Poincaré again described special relativity as the "mechanics of Lorentz":
On the other hand, in a memoir written as a tribute after Poincaré's death, Lorentz readily admitted the mistake he had made and credited Poincaré's achievements:
In summary, Poincaré regarded the mechanics as developed by Lorentz in order to obey the principle of relativity as the essence of the theory, while Lorentz stressed that perfect invariance was first obtained by Poincaré. The modern view is inclined to say that the group property and the invariance are the essential points. CharacterPoincaré's work habits have been compared to a bee flying from flower to flower. Poincaré was interested in the way his mind worked; he studied his habits and gave a talk about his observations in 1908 at the Institute of General Psychology in Paris. He linked his way of thinking to how he made several discoveries. The mathematician Darboux claimed he was un intuitif (intuitive), arguing that this is demonstrated by the fact that he worked so often by visual representation. He did not care about being rigorous and disliked logic. He believed that logic was not a way to invent but a way to structure ideas and that logic limits ideas. Toulouse' characterisationPoincaré's mental organisation was not only interesting to Poincaré himself but also to Toulouse, a psychologist of the Psychology Laboratory of the School of Higher Studies in Paris. Toulouse wrote a book entitled Henri Poincaré (1910). In it, he discussed Poincaré's regular schedule:
However, these abilities were somewhat balanced by his shortcomings:
In addition, Toulouse stated that most mathematicians worked from principles already established while Poincaré started from basic principles each time. (O'Connor et al., 2002) His method of thinking is well summarised as: Habitué à négliger les détails et à ne regarder que les cimes, il passait de l'une à l'autre avec une promptitude surprenante et les faits qu'il découvrait se groupant d'eux-mêmes autour de leur centre étaient instantanément et automatiquement classés dans sa mémoire. (He neglected details and jumped from idea to idea, the facts gathered from each idea would then come together and solve the problem.) (Belliver, 1956) ShortcomingsAlthough a brilliant researcher, Poincaré was resistant to contributions from mathematicians like Georg Cantor and saw mathematical work in economics and finance as peripheral. In 1900 Poincaré commented on Louis Bachelier's thesis "The Theory of Speculation", saying: "M. Bachelier has evidenced an original and precise mind [but] the subject is somewhat remote from those our other candidates are in the habit of treating." (Bernstein, 1996, p.199-200) However, Bachelier's work explained what was then the French government's pricing options on French Bonds and anticipated many of the pricing theories in financial markets used even today.[citation needed] HonoursAwards
Named after him
PublicationsPoincaré's major contribution to algebraic topology was Analysis situs (1895), which was the first real systematic look at topology. He published two major works that placed celestial mechanics on a rigorous mathematical basis:
In popular writings he helped establish the fundamental popular definitions and perceptions of science by these writings:
PhilosophyPoincaré had the opposite philosophical views of Bertrand Russell and Gottlob Frege, who believed that mathematics was a branch of logic. Poincaré strongly disagreed, claiming that intuition was the life of mathematics. Poincaré gives an interesting point of view in his book Science and Hypothesis:
Poincaré believed that arithmetic is a synthetic science. He argued that Peano's axioms cannot be proven non-circularly with the principle of induction (Murzi, 1998), therefore concluding that arithmetic is a priori synthetic and not analytic. Poincaré then went on to say that mathematics cannot be deduced from logic since it is not analytic. His views were the same as those of Kant (Kolak, 2001). However Poincaré did not share Kantian views in all branches of philosophy and mathematics. For example, in geometry, Poincaré believed that the structure of non-Euclidean space can be known analytically. Poincaré held that conventions play an important role in physics. His view (and some later, more extreme versions of it) came to be known as "conventionalism." Poincaré believed that Newton's first law was not empirical but is a conventional framework assumption for mechanics. He also believed that the geometry of physical space is conventional. He considered examples in which either the geometry of the physical fields or gradients of temperature can be changed, either describing a space as non-Euclidean measured by rigid rulers, or as a Euclidean space where the rulers are expanded or shrunk by a variable heat distribution. However, Poincaré thought that we were so accustomed to Euclidean geometry that we would prefer to change the physical laws to save Euclidean geometry rather than shift to a non-Euclidean physical geometry. See also
Notes2Lorentz (1904) had written 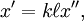 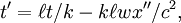 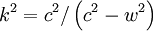 . Later in the paper he deduced that . Later in the paper he deduced that 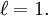 Lorentz's Lorentz's 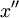 was, in Poincaré's notation, equal to x − wt. Eliminating was, in Poincaré's notation, equal to x − wt. Eliminating 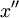 and putting and putting 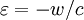 yields the Lorentz transformations as Poincaré wrote them. yields the Lorentz transformations as Poincaré wrote them.
ReferencesThis article incorporates material from Jules Henri Poincaré on PlanetMath, which is licensed under the GFDL. General references
References to work on relativity
Galison, P. (2003) Einstein's Clocks, Poincare's Maps.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Henri_Poincaré". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





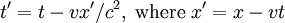
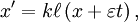
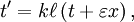
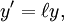
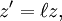
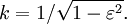
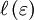 must be unity for all
must be unity for all 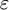 (Lorentz had set
(Lorentz had set 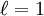 by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination
by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination 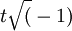 as the coordinates of a space of four dimensions, the transformations of relativity are reduced to rotations in that space. [emphasis added]
as the coordinates of a space of four dimensions, the transformations of relativity are reduced to rotations in that space. [emphasis added]


