To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Lorentz ether theoryWhat is now called Lorentz Ether theory ("LET") has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century. An extension of the theory was developed in particular by Henri Poincaré, who coined the name "The New Mechanics" for Lorentz's theory. One of its features was to explain why no experiments had been able to detect any motion relative to an immobile aether, which was done by introducing the Lorentz transformation. Many aspects of Lorentz's theory were incorporated into special relativity (SR) with the works of Albert Einstein and Hermann Minkowski. Today LET is often treated as some sort of "Lorentzian" or "neo-Lorentzian" interpretation of special relativity. Introducing the effects of length contraction and time dilation in a "preferred" frame of reference leads to the Lorentz transformation and therefore it is not possible to distinguish between LET and SR by experiment. However, in LET the existence of an undetectable ether is assumed and the validity of the relativity principle seems to be only coincidental, which is one reason why SR is commonly preferred over LET. Product highlight
Historical developmentBasic concept
This theory, which was developed mainly between 1892 and 1906 by Lorentz and Poincaré, was based on the aether theory of Augustin-Jean Fresnel, Maxwell's equations and the electron theory of Rudolf Clausius.[1] Lorentz introduced a strict separation between matter (electrons) and ether, whereby in his model the ether is completely motionless, and it won't be set in motion in the neighbourhood of ponderable matter. As Max Born later said, it was natural (though not logically necessary) for scientists of that time to identify the rest frame of the Lorentz ether with the absolute space of Isaac Newton.[2] The condition of this ether can be described by the electric field E and the magnetic field H, where these fields represent the "states" of the ether (with no further specification), related to the charges of the electrons. Thus an abstract electromagnetic ether replaces the older mechanistic ether models. Contrary to Clausius, who accepted that the electrons operate by actions at a distance, the electromagnetic field of the ether appears as a mediator between the electrons, and changes in this field can propagate not faster than the speed of light. Lorentz theoretically explained the Zeeman effect on the basis of his theory, for which he received the Nobel Prize in Physics in 1902. It must be empathized that Joseph Larmor found a similar theory simultaneously, but his concept was based on a mechanical ether.[3]
A fundamental concept of Lorentz's theory in 1895[4] was the "theorem of corresponding states" for terms of order v/c. This theorem states that a moving observer (relative to the ether) in his „fictitious“ field makes the same observations as a resting observers in his „real“ field. This theorem was extended for terms of all orders by Lorentz (1904)[5] and completed by Poincaré (1905, 1906)[6][7] and by Lorentz (1906, 1916)[8] in order to obey the principle of relativity. Length contractionA big challenge for this theory was the Michelson–Morley experiment in 1887. According to the theories of Fresnel and Lorentz a relative motion to an immobile ether had to be determined by this experiment, however, the result was negative. [9] In 1888 Oliver Heaviside derived from the Maxwell equations that the electrostatic field around a moving, spherical body is contracted in the line of motion by the factor
The so called Length contraction without expansion perpendicularly to the line of motion and by the precise value Local timeAn important part of the theorem of corresponding states was the local time t' = t − vx / c2, where t is the time coordinate for an observer resting in the ether, and t' is the time coordinate for an observer moving in the ether. (Woldemar Voigt used the same expression for local time already in 1887[14] in connection with the Doppler effect and an incompressible medium.) While for Lorentz length contraction was a real physical effect, he considered the time transformation only as a heuristic working hypothesis and a mathematical stipulation. With the help of this concept Lorentz could explain the aberration of light, the Doppler effect and the measurements of the Fresnel drag coefficient by Hippolyte Fizeau in moving and resting liquids as well. In contrast, Poincaré saw more than a mathematical trick in the definition of local time, which he called Lorentz's "most ingenious idea".[15] In 1898 he wrote:[16]
In 1900 Poincaré interpreted local time as the result of a synchronisation procedure based on light signals. He assumed that 2 observers A and B which are moving in the ether, synchronize their clocks by optical signals. Since they believe to be at rest they must consider only the transmission time of the signals and than crossing their observations to examine whether their clocks are synchronous. However, from the point of view of an observer at rest in the ether the clocks are not synchronous and indicate the local time t' = t − vx / c2. But because the moving observers don't know anything about their movement, they don't recognize this.[18] In 1904 he illustrated the same procedure in the following way: A sends a signal at the time 0 to B, which arrives at the time t. B also sends a signal at the time 0 to A, which arrives at the time t. If in both cases t has the same value the clocks are synchronous, but only in the system in which the clocks are at rest in the ether. So according to Darrigol[19] and Jannsen,[20] Poincaré understood local time as a physical effect just like length contraction - in contrast to Lorentz, who used the same interpretation not before 1906. However, contrary to Einstein, who later used a similar synchronisation procedure which was called Einstein synchronisation, he still was the opinion that only clocks resting in the ether are showing the „true“ time.[15] However, at the beginning it was unknown that local time includes what is now known as time dilation. This effect was first noticed by Larmor (1897),[3] who wrote that "individual electrons describe corresponding parts of their orbits in times shorter for the [ether] system in the ratio Lorentz transformation
In 1887[14] Voigt derived a similar form of equations (with a wrong scale factor), which later were known as the Lorentz transformation. Based on his theorem of corresponding states, also Lorentz in 1895[4] was in possession of the first order variant of those equations. Larmor in 1897[3] and Lorentz in 1899[21] adjusted them to account for second order effects and gave them a algebraically equivalent form to those, which are used up to this day (however, Lorentz used an undetermined factor l in his transformation). In 1904[5] Lorentz came very near to create such a theory, where all forces between the molecules, whatever their nature may be, are affected by the Lorentz transformation (in which Lorentz set the factor l to unity) in the same manner as electrostatic forces. This step had become necessary due to other unsuccessful ether drift experiments like the Trouton–Noble experiment. However, on 5 Juni 1905[7] Poincaré showed that Lorentz equations of electrodynamics were not fully Lorentz covariant. So by pointing out the group characteristics of the transformation Poincaré demostrated the Lorentz covariance of the Maxwell-Lorentz equations by correcting Lorentz's formulae for the transformations of charge density and current density. He also sketched a model of gravitation (incl. gravitational waves) which might be compatible with the transformations. Poincaré used for the first time the term "Lorentz transformation", and he gave them a form which is used up to this day. (Where A substantially extended work (the so called „Palermo paper“)[6] was submitted by Poincaré on 23 July 1905, but was published on January 1906, because the journal only appeared two times in a year. He spoke literally of „the postulate of relativity“, he showed that the transformations are a consequence of the principle of least action; he demonstrated in more detail the group characteristics of the transformation, which he called Lorentz group, and he showed that the combination x2 + y2 + z2 − c2t2 is invariant. While elaborating his gravitational theory he noticed that the Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing Principles and conventions
Light postulateAlready in his philosophical writing on time measurements (1898)[16] Poincaré wrote that astronomers like Ole Rømer, in determining the speed of light, simply assume that light has a constant speed, and that this speed is the same in all directions. Without this postulate it would not be possible to infer the speed of light from astronomical observations, as Rømer did based on observations of the moons of Jupiter. Poincaré went on to note that Rømer also had to assume that Jupiter's moons obey Newton's laws, including the law of gravitation, whereas it would be possible to reconcile a different speed of light with the same observations if we assumed some different (probably more complicated) laws of motion. According to Poincaré, this illustrates that we adopt for the speed of light a value that makes the laws of mechanics as simple as possible. (This is an example of Poincaré's conventionalist philosophy.) Poincaré also noted that the propagation speed of light can be (and in practice often is) used to define simultaneity between spatially separate events. However, in that paper he did not go on to discuss the consequences of applying these "conventions" to multiple relatively moving systems of reference. This next step was done by Poincaré in 1900,[18] when he recognized that synchronisation by light signals in earth's reference frame leads to Lorentz's local time. (See the section on "local time" above). Principle of relativityAlready in 1895[23] Poincaré argued that experiments like that of Michelson-Morley show that it seems to be impossible to detect the absolute motion of matter or the relative motion of matter in relation to the ether. And although most physicists at this time believed that the "principle of relative motion" was incompatible with the ether, Poincaré stated in 1900[24] that he did not believe that the relative speed of the earth to the ether will ever be measured. In 1904[15] he appreciated the work of the mathematicians, who saved what he now called the "principle of relativity" with the help of hypotheses like local time, but he confessed that this venture was possible only by an accumulation of hypotheses. And he defined the principle in this way:
Referring to a critique of Poincaré in 1900,[24] who said that it would be better to create a more fundamental theory than to create one hypothesis after the other, Lorentz wrote in his famous paper in 1904, where he extended his theorem of corresponding states:[5]
One of the first assessments of Lorentz's paper was by Paul Langevin in May 1905.[25] According to him, this extension of the electron theories of Lorentz and Larmor led to "the physical impossibility to demonstrate the translational motion of the earth". Although Poincaré showed in 1905,[7] that Lorentz didn't completed his task, he attributed this postulate to Lorentz:
In the Palermo paper (1906), Poincaré called this "the postulate of relativity“, and although he stated that it was possible this principle might be disproved at some point (and in fact he mentioned at the paper's end that the discovery of magneto-cathode rays seems to threaten it), he believed it was interesting to consider the consequences if we were to assume the postulate of relativity was valid without restriction. This would imply that all forces of nature (not just electromagnetism) must be invariant under the Lorentz transformation.[6] In 1921 Lorentz credited Poincaré for establishing the principle and postulate of relativity and wrote:[27]
EtherPoincaré wrote in the sense of his conventionalist philosophy in 1889: [29]
He also denied the existence of absolute space and time by saying in 1901:[30]
However, Poincaré himself never abandoned the ether hypothesis and stated in 1900,[24] that the ether is needed to explain where the ray of light is after leaving the source and before reaching the receiver. In order not to give up the comfort of the simplicity of the mechanical laws of nature and because in mechanics all conditions must be determined by preceding conditions, a material carrier is needed. And although he admitted the relative and conventional character of space and time, he believed that the classical convention is more "convenient" and continued to distinguish between "true" time in the ether and "apparent" time in moving systems. Adressing the question if a new convention of space and time is needed he wrote in 1912:[31]
Also Lorentz argued during his lifetime that in all frames of reference this one has to be preferred, in which the ether is at rest. Clocks in this frame are showing the "real“ time and simultaneity is not relative. However, if the correctness of the relativity principle is accepted, it is impossible to find this system by experiment.[32] Mass, energy and speedRest mass and energyIt was recognized by J. J. Thomson in 1881[33] that a charged body is harder to set in motion than an uncharged body, which was worked out on more detail by Heaviside (1889) and George Frederick Charles Searle (1896).[34] So the electrostatic energy behaves as having some sort of electromagnetic mass, which can increase the normal mechanical mass of the bodies. This was discussed in connection with the proposal of the electrical origin of matter, and Wilhelm Wien (1900),[35] Max Abraham (1902),[36] and Lorentz (1904)[5] came to the conclusion that the total mass of the bodies is identical to its electromagnetic mass. And because the em-mass depends on the em-energy, the formula for the energy-mass-relation given by Wien (1900) was m = (4 / 3)E / c2 (Abraham and Lorentz used similar expressions). Wien stated, that if it is assumed that gravitation is an electromagnetic effect too, than there has to be a proportionality between em-energy, inertial mass and gravitational mass. However, it was not recognized that energy can transport inertia from one body to another and that mass can be converted into energy, which was explained by Einstein's mass–energy equivalence - see „The shift to relativity“. The idea of an electromagnetic nature of matter had to be given up, however, in the course of the development of relativistic mechanics. It turned out that different results occurred, dependent on whether the em-mass is calculated from the energy or from the momentum, and the 4/3-factor had to be compensated as well. To solve those problems, and also to explain the stability of Lorentz's matter-electron configuration, Poincaré in 1905[7] and 1906[6] introduced some sort of pressure of non-electrical nature, which contributes the amount − (1 / 3)E / c2 to the mass of the bodies, and therefore the 4/3-factor vanishes. Max von Laue showed in 1910 that Poincaré's model is only one of many possible compensation mechanisms.[20] Mass and speedThomson, Heaviside and Searle also noticed that inertia depends on the speed of the bodies as well. In 1899 Lorentz calculated that the ratio of the electron masses of the moving frame and the ether frame is
This theory was further developed by Abraham (1902), who first used the terms longitudinal and transverse mass for Lorentz's two masses. However, Abraham's expressions were more complicated than those of Lorentz.[36] Lorentz himself expanded his 1899 ideas in his famous 1904 paper, where he set the factor Poincaré wrote in 1904, that because of the variability of mass the conservation of mass isn't valid anymore. In a later edition of his book Science and Hypothesis in 1906 he concluded that in case matter is of electromagnetic origin, and because matter and mass are inseparably connected, matter doesn't exist at all and electrons are only concavities in the ether. In 1908 Poincaré illustrated this kind of inertia by a body which moves in a liquid. If the body changes the direction it suffers resistance, afterwards it moves in straight lines, because the resistance is compensated by some sort of wake (in that case the electromagnetic fields). With each acceleration this energy must be supplied too.[38] The mass concept of Lorentz (incl. longitudinal and transverse mass) was incorporated into special relativity by Einstein (1905)[39] and Max Planck (1906).[40] In 1905 Kaufmann conducted another series of experiments, which confirmed Abraham's theory, but contradicted what Kaufmann called the "Lorentz-Einstein theory".[41] However, in the following years experiments by Bucherer (1908) and others confirmed Lorentz's mass formula.[42] Later a similar concept was also used as relativistic mass by reputable physicists like Max Born[2] and Wolfgang Pauli[43] and is sometimes used in physics textbooks up to this day, although the expression invariant mass is preferred. Inertia of energyJames Clerk Maxwell (1874) [44] and Adolfo Bartoli (1876) [45] found out that the existence of tensions in the ether like the radiation pressure follows from the electromagnetic theory. Lorentz recognized in 1895[4] that this is also the case in his theory. So if the ether is able to set bodies in motion, the action/reaction principle demands that the ether must be set in motion by matter as well. However, Lorentz pointed out the this is impossible, because any tension in the ether requires the mobility of the ether parts, which in not possible in his immobile ether. This represents a violation of the reaction principle which was accepted by Lorentz consciously. He continued by saying, that one can only speak about fictitious tensions, since they are only mathematical models in his theory to ease the description of the electrodynamic interactions. In 1900[18] Poincaré studied the conflict between the action/reaction principle and Lorentz's theory. He tried to determine whether the center of gravity still moves with a uniform velocity when electromagnetic fields are included. He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. The electromagnetic field energy behaves like a fictitious fluid („fluide fictif“) with a mass density of E / c2 (in other words m = E / c2). If the center of mass frame (COM-frame) is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible - it's neither created or destroyed - then the motion of the center of mass frame remains uniform. But electromagnetic energy is not indestructible and can be converted into other forms of energy, and therefore loses its mass (which was the reason why Poincaré regarded em-energy as a "fictitious" fluid rather than a "real" fluid). So Poincaré assumed that there exists a non-electric energy fluid at each point in the ether, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the COM-frame (incl. matter, em-energy and non-electrical energy) remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions. But Poincaré's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a recoil from the inertia of the fictitious fluid. In the framework of Lorentz's theory Poincaré performed a Lorentz boost to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold.[19] Poincaré came back to this topic in „Science and Hypothesis“ (1902) and „The Value of Science“ (1905). This time he rejected the possibility that energy carries mass and thereby rejected his own solution, that motions in the ether can compensate the motion of matter:[15]
Besides this radiation paradox (1) he also discussed two other problematic effects: (2) non-conservation of mass implied by Abraham's and Lorentz's theory of variable mass, and Kaufmann's experiments on the mass of fast moving electrons and (3) the non-conservation of energy in the radium experiments - however, for the latter he cited William Ramsay's proposal that radium is transformed because it contains an enormous amount of energy. Even in 1908, he rejected the idea that energy is carrying mass and used the same arguments as in 1904 in order to show that the reaction principle is not valid in the new mechanics.[38] Those problems were later solved through Einstein's mass–energy equivalence - see "The shift to relativity". Following Poincaré, Abraham introduced the term „electromagnetic momentum“ to maintain the reaction principle, whereby the field density per cm3 is E / c2 and E / c per cm2.[36] In 1904, Friedrich Hasenöhrl concluded that radiation contributes to the inertia of bodies, and inertia depends on temperature as well.[46] He derived the formula m = (8 / 3)E / c2, where m is the "apparent mass" due to radiation. This was corrected in 1905 by Abraham and him to m = (4 / 3)E / c2 (the same formula as for the electromagnetic mass, see section „Mass and speed“). GravitationLorentz's theoriesIn 1900[47] Lorentz tried to explain gravity on the basis of the Maxwell equations. He first considered a Le Sage type model and argued that there possibly exists an universal radiation field, consisting of very penetrating em-radiation, and exerting an uniform pressure on every body. Lorentz showed that an attractive force between charged particles would indeed arise, if it is assumed that the incident energy is entirely absorbed. This was the same fundamental problem which had afflicted the other Le Sage models, because the radiation must vanish somehow and any absorption must lead to an enormous heating. Therefore Lorentz abandoned this model. In the same paper, he assumed like Ottaviano Fabrizio Mossotti and Johann Karl Friedrich Zöllner that the attraction of opposite charged particles is stronger than the repulsion of equal charged particles. The resulting net force is exactly what is known as universal gravitation, in which the speed of gravity is that of light. This leads to a conflict with the law of gravitation by Isaac Newton, in which it was shown by Pierre Simon Laplace that a finite speed of gravity leads to some sort of aberration and therefore makes the orbits unstable. However, Lorentz showed that the theory is not concerned by Laplace's critique, because due to the structure of the Maxwell equations only effects in the order v2/c2 arise. But Lorentz calculated that the value for the perihelion advance of Mercury was much too low. He wrote:
In 1908[38] Poincaré examined the gravitational theory of Lorentz and classified it as compatible with the relativity principle, but (like Lorentz) he criticized the inaccurate indication of the perihelion advance of Mercury. Contrary to Poincaré, Lorentz in 1914 considered his own theory as incompatible with the relativity principle and rejected it.[48] Lorentz-invariant gravitational lawPoincaré argued in 1904 that a propagation speed of gravity which is greater than c is contradicting the concept of local time and the relativity principle. He wrote: [15]
However, in 1905 and 1906 Poincaré pointed out the possibility of a gravitational theory, in which changes propagate with the speed of light and which is Lorentz covariant. He pointed out that in such a theory the gravitational force not only depends on the masses and their mutual distance, but also on their velocities and their position due to the finite propagation time of interaction. On that occasion Poincaré introduced four-vectors.[7] Following Poincaré, also Minkowski (1908) and Arnold Sommerfeld (1910) tried to establish a lorentz-invariant gravitational law.[22] However, these attempts were superseded because of Einstein's theory of general relativity, see "The shift to relativity". The shift to relativity
Special relativityIn 1905, Albert Einstein published his paper on what is now called special relativity.[39] In this paper, by examining the fundamental meanings of the space and time coordinates used in physical theories, Einstein showed that the "effective" coordinates given by the Lorentz transformation were in fact the inertial coordinates of relatively moving frames of reference. From this followed all of the physically observable consequences of LET, along with others, all without the need to postulate an unobservable entity (the ether). Einstein identified two fundamental principles, each founded on experience, from which all of Lorentz's electrodynamics follows:
Taken together (along with a few other tacit assumptions such as isotropy and homogeneity of space), these two postulates lead uniquely to the mathematics of special relativity. Lorentz and Poincare had also adopted these same principles, as necessary to achieve their final results, but didn't recognize that they were also sufficient, and hence that they obviated all the other assumptions underlying Lorentz's initial derivations (many of which later turned out to be incorrect [49]). Therefore, special relativity very quickly gained wide acceptance among physicists, and the 19th century concept of a luminiferous ether was no longer considered useful. Einstein's 1905 presentation of special relativity was soon supplemented, in 1907, by Hermann Minkowski, who showed that the relations had a very natural interpretation in terms of a unified four-dimensional "spacetime" in which absolute intervals are seen to be given by an extension of the Pythagorean theorem. (Already in 1906 Poincaré anticipated some of Minkowski's ideas, see the section "Lorentz-transformation"). [50] The naturalness and utility of the representation by Einstein and Minkowski contributed to the rapid acceptance of special relativity, and to the corresponding loss of interest in Lorentz's ether theory. Lorentz argued in 1913, that there is little difference between his ether theory and the negation of a preferred reference frame, as in the theory of Einstein and Minkowski, and therefore according to him it is a matter of taste which theory one prefers.[32] However, in 1907 Einstein criticized the "ad hoc" character of Lorentz's contraction hypothesis in his theory of electrons, because according to him it was only invented to rescue the hypothesis of an immobile ether. Einstein thought it necessary to replace Lorentz's theory of electrons by assuming that Lorentz's "local time" can simply be called "time", and he stated that the immobile ether as the theoretical fundament of electrodynamics was unsatifactory.[51] Minkowski ironically said that for Lorentz the contraction hypothesis is only a "gift from above". And although Lorentz's hypothesis is "completely equivalent with the new concept of space and time", Minkowski held that it becomes much more comprehensible in the framework of the new spacetime physics. Mass–energy equivalenceIt was derived by Einstein (1905) as a consequence of the relativity principle, that inertia of energy is actually represented by E / c2, but in contrast to Poincaré's 1900-paper Einstein recognized, that matter itself loses or gain mass during the emission or absorption.[52] So the mass of any form of matter is equal to a certain amount of energy, which can converted into and re-converted from other forms of energy. This is the mass–energy equivalence, represented by E = mc2. So Einstein didn't have to introduce "fictitious" masses and also avoided the perpetual motion problem, because according to Darrigol[19], Poincaré's radiation paradox can simply be solved by applying Einstein's equivalence. If the light source loses mass during the emission by E / c2, the contradiction in the momentum law vanishes. Similar to Poincaré, Einstein concluded in 1906 that the inertia of (electromagnetic) energy is a necessary condition for the center of mass theorem to hold in systems, in which electromagnetic fields and matter are acting on each other. Based on the mass–energy equivalence he showed that emission and absorption of em-radiation and therefore the transport of inertia solves the problem. On that occasion, Einstein referred to Poincaré's 1900-paper and wrote:[53]
Also Poincaré's rejection of the reaction principle due to the violation of the mass conservation law can be avoided through Einstein's E = mc2, because mass conservation appears as a special case of the energy conservation law. General relativityThe attempts of Lorentz and Poincaré (and other attempts like those of Abraham and Gunnar Nordström) to formulate a theory of gravitation, were superseded by Einstein's theory of general relativity. [22] This theory is based on principles like the equivalence principle, the general principle of relativity, the principle of general covariance, geodesic motion, local Lorentz invariance (the laws of special relativity apply locally for all inertial observers), and that spacetime curvature is created by stress-energy within the spacetime. In 1920 Einstein compared Lorentz's ether with the "gravitational ether" of general relativity. He said that immobility is the only mechanical property of which the ether has not been deprived by Lorentz, but contrary to the luminiferous and Lorentz's ether the ether of general relativity has no mechanical property, not even immobility:[55]
Priority
In a paper that was written in 1914 and published in 1921,[56] Lorentz appreciated the Palermo paper (1906)[6] of Poincaré on relativity. Lorentz stated:
However, a 1916 reprint of his main work "The theory of electrons"[8] contains notes (written in 1909 and 1915) in which Lorentz sketched the differences between his results and that of Einstein as follows:
Regarding the fact, that in this book Lorentz only mentioned Einstein and not Poincaré in connection with a) the synchronisation by light signals, b) the reciprocity of the Lorentz transformation, and c) the relativistic transformation law for charge density, Janssen comments:[20]
And at a conference on the Michelson-Morley experiment in 1927 at which Lorentz and Michelson were present, Michelson suggested that Lorentz was the initiator of the theory of relativity. Lorentz then replied:[58]
Poincaré attributed the development of the new mechanics almost entirely to Lorentz. He only mentioned Einstein in connection with the photoelectric effect, but not in connection with special relativity. For example, in 1912 Poincaré raises the question whether „the mechanics of Lorentz“ will still exist after the development of the quantum theory. He wrote: [59]
In his well-known „History of the theories of ether and electricity“ from 1953, E. T. Whittaker claimed that relativity is the creation of Lorentz and Poincaré and attributed to Einstein's papers only little importance.[60] However, the predominant majority of the historians of science like Abraham Pais,[61] John Stachel[62] or Olivier Darrigol[19] and physicists like Born[2] or Pauli[43] have other points of view. It's true that Lorentz and Poincaré developed the mathematics of special relativity, and many scientists originally spoke about the „Lorentz-Einstein theory“. But Einstein was the first (contrary to Lorentz and Poincaré) to banish the (classical) ether out of physics, which lead to a fundamental new approach to physics. Einstein wrote in 1907[51] that one needed only to realize that an auxiliary quantity that was introduced by Lorentz and that he called "local time" can simply be defined as "time." And in 1910[63] and 1912[64] Einstein explained that he borrowed the principle of the constancy of light from Lorentz's immobile ether, but he recognized that this principle together with the principle of relativity makes the ether useless and leads to special relativity. It is also known[65] that he read Poincaré's 1902-book „Science and hypothesis“ before 1905, which included:
Einstein refers to Poincaré in connection with the inertia of energy in 1906[53] and the non-Euclidean geometry in 1921,[55] but not in connection with the Lorentz transformation, the relativity principle or the synchronisation procedure by light signals. However, in the last years before Einstein's death he acknowledged some of Poincaré's contributions (according to Darrigol, maybe because his biographer Pais in 1950 sent him a copy of Poincarè's Palermo paper, which he hadn't read before). Einstein wrote in 1953:
Recent activityNeo-Lorentzian interpretationsToday LET is often treated as some sort of "neo-Lorentzian" interpretation of special relativity. For example, Reza Mansouri and Roman Ulrich Sexl (1977)[66] created a "test theory" of special relativity, in order to establish the framework for examinations about the validity of the Lorentz symmetry and the existence of a preferred frame of reference. By setting the speed of light to unity they chose the following coefficients of the transformation between reference frames:
Where T, X are coordinates measured in the (preferred) ether frame, and t, x are coordinates measured in a moving frame, and therefore 1 / a(v) is time dilation and b(v) is length contraction. By supposing
So Sexl/Mansouri spoke about the "remarkable result that a theory maintaining absolute simultaneity is equivalent to special relativity." However they preferred SRT over an ether theory, because the latter "destroys the internal symmetry of a physical theory". Breaking Lorentz symmetry?However, there are some models, which predict a violation of the Lorentz symmetry and which have some similarity to LET, although they are not the same. Modern measurements empirically seems to discredit such theories. A 2007 study sensitive to 10-16 employed two simultaneous interferometers over a year's observation: Optical in Berlin, Germany at 52°31'N 13°20'E and microwave in Perth, Australia at 31°53'S 115°53E. Such an aether background (leading to Lorentz violation) could never be at rest relative to both of them. [67] Affine (Einstein-Cartan theory), teleparallelism (Weitzenböck) and noncommutative (Alain connes) gravitation theories wholly contain General Relativity as a restricted case (isotropic vacuum, Equivalence Principle = true). They also allow a Lorentz-violating chiral vacuum background (anisotropic vacuum) in which the Equivalence Principle has parity violations in the mass sector (e.g., enantiomorphic mass distributions - atom locations - in opposite parity space groups P3121 and P3221 chemically identical crystals). This is experimentally unexamined. BibliographyPrimary sources
Secondary sources
Endnotes
Categories: Aether theories | Obsolete scientific theories |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lorentz_ether_theory". A list of authors is available in Wikipedia. |





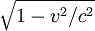 .
.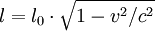 (where l0 is the length at rest in the ether) was given by Larmor in 1897
(where l0 is the length at rest in the ether) was given by Larmor in 1897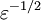 or
or 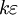 times as great as in S0", where S0 is the ether frame, k is
times as great as in S0", where S0 is the ether frame, k is 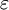 is an undetermined factor.
is an undetermined factor. 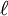 is an arbitrary function of
is an arbitrary function of 
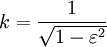
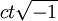 as a fourth imaginary coordinate, and he used an early form of four-vectors. However, Poincaré later said the translation of physics into the language of four-dimensional metry would entail too much effort for limited pro?t, and therefore he refused to work out the consequences of this notion.
as a fourth imaginary coordinate, and he used an early form of four-vectors. However, Poincaré later said the translation of physics into the language of four-dimensional metry would entail too much effort for limited pro?t, and therefore he refused to work out the consequences of this notion.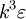 parallel to the direction of motion and
parallel to the direction of motion and 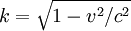 and
and 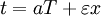
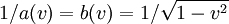 the Lorentz transformation follows. Then they discussed different methods of clock synchronisation.
the Lorentz transformation follows. Then they discussed different methods of clock synchronisation.


