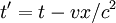To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Relativity of simultaneityThe relativity of simultaneity is the concept that simultaneity is not absolute, but dependent on the observer. That is, according to the special theory of relativity formulated by Albert Einstein in 1905, it is impossible to say in an absolute sense whether two events occur at the same time if those events are separated in space. Where the event occurs in a single place—for example, in a car crash—all observers wherever they are can agree that one car crashed with the other at the same time. But where the events are separated in space, such as one car crashing in America and another in Australia, the question of whether such events are simultaneous is relative; some may calculate the two accidents as happening "at the same time" and others, looking at the events while in a different state of motion, will view the American crash as occurring first, while still others can view the Australian crash as occurring first. Einstein's special theory demonstrates that there are occasions when there is no "correct" answer, where no observer has a privileged status, and all the observers can claim to be "correct" even if their ordering of events disagree with each other. If we imagine one observer who calculates that two events—at different points in space—occur at precisely the same time, an observer who is moving relative to the first will generally disagree, having calculated the two events as occurring at different times. This notion is illustrated in the ladder paradox, a thought experiment which uses the example of a ladder moving at high speed through a garage. A form of the relativity of simultaneity was introduced by Hendrik Lorentz in 1895 (Lorentz's "local time"), but the idea was not widely understood in its modern form until Einstein's introduction of special relativity. In particular, Einstein deduced the failure of absolute simultaneity from two stated assumptions:
A number of scientists have pointed out that some of the predicted consequences of quantum mechanics appear to be incompatible with relativity of simultaneity because of nonlocality, in particular in the case of quantum entanglement[citation needed]. This issue has not yet been resolved. Product highlight
The train-and-platform thought experimentA popular picture for understanding this idea is provided by Einstein's thought experiment consisting of a moving train with one observer midway in the train, and another observer midway on the platform as the train moves past. Here we will present a slightly modified version. A flash of light is given off at the center of the train just when the two observers pass each other. The observer on the train sees the front and back of the train at fixed distances away from the source of the light flash (since the front, back, and train observer are all in the same inertial frame). According to this observer, the light flashes reach the front and back of the train at precisely the same instant of time—that is, simultaneously. On the other hand, the observer on the platform sees the back of the train moving toward the point at which the flash was given off, and the front of the train moving away from it. This means that the light flash going toward the back of the train will have less distance to cover than the light flash going to the front. As the speed of light is finite, and the same in any direction relative to the platform (regardless of the motion of its source), the flashes will not strike the ends of the train simultaneously. This is the key image in understanding this concept, so let's move through it in more detail. A strobe light in the middle of the train pulses once, emitting light in all directions. Some of this light begins its journey towards the back of the train, and some of it heads towards the front, but the source is the same. To the platform observer, the back of the train closes some distance between the original source point (not the current position of the source device itself, which will move) before the light strikes the back of the train. To the train observer, however, the light appears to have traveled the exact distance from the source to the back of the train, and no less. Conversely, the platform observer sees light cover a greater distance to the front of the train, in less time but at the same speed observed by the train observer. For both observers, the speed at which the light traveled is constant, but the distance traveled (and thus the time consumed in covering the distance) varies depending on the relative motion of the observer. Now, we might try to decide if one observer is right and the other wrong. However, Einstein's other assumption is that the two inertial frames (the platform vs. the moving train) must operate under equivalent physical laws. This means that neither one can be shown wrong, and that a simultaneity in one inertial frame need not be true outside that frame.
Spacetime diagramsIt is sometimes helpful to visualize this situation with spacetime diagrams. For a given observer, the t-axis is defined to be a point traced out in time by the origin of the spatial coordinate x, and is drawn vertically. The x-axis is defined as the set of all points in space at the time t=0, and is drawn horizontally. The statement that the speed of light is the same for all observers is represented by drawing a light ray as a 45° line, regardless of the speed of the observer. In the first diagram, we see the two ends of the train drawn as red lines. Because the ends of the train are stationary with respect to the observer on the train, these lines are just vertical lines, showing their motion through time but not space. The flash of light is shown as the 45° yellow lines. We see that the points at which the two light flashes hit the ends of the train are at the same level in the diagram. This means that the events are simultaneous. In the second diagram, we see the two ends of the train moving to the right, shown by parallel lines. The flash of light is given off at a point exactly halfway between the two ends of the train, and again form two 45° lines, expressing the constancy of the speed of light. In this picture, however, the points at which the light flashes hit the ends of the train are not at the same level; they are not simultaneous. The dashed blue line between the events of the light beams hitting the ends of the trains identifies a volume of simultaneity for the observer on the train, i.e. those events which he calculates occur at the same instant of time (these form a flat 3-dimensional surface). Note that for the observer on the platform, each point on that line (identifying a plane where y and z coordinates are the same) is on a different level. So each point on that dashed blue line exists at different time for the station observer, and at the same time for the observer on the train. That is the essence of the relativity of simultaneity. Lorentz transformationsThe relativity of simultaneity can be calculated using Lorentz transformations, which relate the coordinates used by one observer to coordinates used by another in uniform relative motion with respect to the first. Assume that the first observer uses coordinates labeled t, x, y, and z, while the second observer uses coordinates labeled t', x', y', and z'. Now suppose that the first observer sees the second moving in the x-direction at a velocity v. And suppose that the observer's coordinate axis are parallel and that they have the same origin. Then, the Lorentz transformations show that the coordinates are related by the equations where c is the speed of light. If two events happen at the same time in the frame of the first observer, they will have identical values of the t-coordinate. However, if they have different values of the x-coordinate (different positions in the x-direction), we see that they will have different values of the t' coordinate; they will happen at different times in that frame. The term that accounts for the failure of absolute simultaneity is that
The equation t'=constant defines a "line of simultaneity" in the (x', t') coordinate system for the second (moving) observer, just as the equation t=constant defines the "line of simultaneity" for the first (stationary) observer in the (x,t) coordinate system. We can see from the above equations for the Lorentz transform that t' is constant if and only if Graphically, this can be represented on a space-time diagram by the fact that a plot of the set of points regarded as simultaneous generates a line which depends on the observer. In the space-time diagram at the right, the dashed line represents a set of points considered to be simultaneous with the origin by an observer moving with a velocity v of one-quarter of the speed of light. The dotted horizontal line represents the set of points regarded as simultaneous with the origin by a stationary observer. This diagram is drawn using the (x,t) coordinates of the stationary observer, and is scaled so that the speed of light is one, i.e. so that a ray of light would be represented by a line with a 45 degree angle from the x axis. From our previous analysis, given that v=0.25 and c=1, the equation of the dashed line of simultaneity is Evolution of the conceptAt the time that special relativity was introduced, relativity of simultaneity already existed as a practical concept. By the end of 19th century, light was conceived as a wave phenomenon, propagating a certain velocity with respect to the Luminiferous ether. Astronomers could not determine the true one-way speed of light relative to the solar system; instead they simply took the speed of light to be isotropic relative to their frame of reference. In a discussion about the problem of establishing simultaneity, Poincaré wrote in "La Mesure du Temps"(1898) about that "opportunistic" approach: "When an astronomer tells me that a stellar phenomenon that his telescope reveals to him at this moment, nevertheless occurred fifty years ago, I try to find out what he tries to say and for this reason, I will ask him initially how he knows it, i.e. how he measured the speed of the light. He started by assuming that the light has a constant speed, and in particular that its speed is the same in all directions. That is a postulate without which no measurement of this speed could be attempted." A sophisticated experiment with light signals, the Michelson Morley experiment, failed to detect motion relative to the ether and it was soon proposed that length contraction made this impossible—a conspiracy of nature that makes it impossible to establish absolute simultaneity in this way. One could think that instead a time dissemination procedure using portable clocks would yield an unambiguous result. One could synchronize portable clocks and move them a distance apart. However, Poincaré stressed that such is based on the postulate that clock rate is fully unaffected by such clock transport. For clocks to be perfectly synchronized for more than an instant, they must count units of time at the same rate, and they must simultaneously indicate the same time. As chronometers became more and more refined the differences became smaller and smaller. This instilled confidence that no matter where a traveling clock is, and no matter how it arrived at where it is, it can be absolutely in synchrony with a universal time-keeping. In contrast, efforts to formulate a comprehensive theory of motion for electrons brought theorists such as Larmor, Lorentz, Poincaré and Einstein to a point where there seemed to be persuasive evidence that for electromagnetic as well as mechanical mechanisms the rate of clock time is not fixed, but a function of speed. According to the special theory of relativity, clocks that are in motion do not measure time at the same rate. They suffer an effect called time dilation; so that the faster they move, the more their rate is slowed. Consequently, the path that the clock takes from one event to another affects the amount of time which it indicates has passed. One would like to make a correction for such an effect just as one might correct for variations caused by temperature or the local acceleration of gravity. However, such a correction would require knowing one's absolute velocity which is impossible to determine. Special relativity predicts that all procedures, either using portable clocks or using signals to maintain synchronized time-keeping, yield results that cannot be distinguished from those which would be seen if the same experiment were done in a frame of reference which is at absolute rest. As a result no concept of absolute simultaneity can be defined and one is forced to use a concept of relativity of simultaneity. Consequently, we can abandon the attempt to correct for the motion of our reference frame and limit our corrections to those which would be used if the reference frame were at absolute rest. We can still correct for time dilation, but we assume the motion of the clock is only relative to the reference frame. We can correct for signal delay, but we assume that the light signal moves at the same speed in all directions. Relativity of simultaneity and "local time"In 1898 (La Mesure du Temps), Henri Poincaré discussed in this context the light postulate as quoted above, based on which simultaneity was established by convention. In 1900 Poincaré was more explicit about the "new rule" for establishing simultaneity. He remarked that Lorentz's "wonderful invention", "local time", arose when clocks in a moving reference frame are synchronized by exchanging signals which are assumed to travel with the same speed in both directions, a procedure now familiar from the special theory of relativity. His illustration neglects length contraction and time dilation. Such second order effects can be neglected on the assumption that all object speeds are much smaller than that of light ( We suppose that the Earth is moving with speed v in the x-direction in some rest system which corresponds to the "local time" as used by Lorentz. As can be seen in he Lorentz Transformation equations, apart of inertial coordinate systems only space and time enter into the theory. Thus relativity of simultaneity becomes a property of Minkowski space. Einstein (1934) was clear that there was no need to talk of an aether:
In this regard Lorentz' earlier quote (1927) is also notable:
References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Relativity_of_simultaneity". A list of authors is available in Wikipedia. |





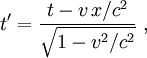
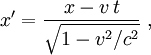
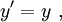
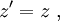
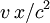 .
.
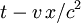 = constant. Thus the set of points that make t constant are different than the set of points that makes t' constant. That is, the set of events which are regarded as simultaneous depends on the frame of reference used to make the comparison.
= constant. Thus the set of points that make t constant are different than the set of points that makes t' constant. That is, the set of events which are regarded as simultaneous depends on the frame of reference used to make the comparison.
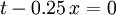 and with v=0, the equation of the dotted line of simultaneity is
and with v=0, the equation of the dotted line of simultaneity is 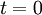 .
.
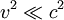 ).
).
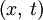 (i.e. the
(i.e. the 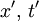 frame) we send a light signal from one clock (at the origin) to the other and bounce it back.
Then we obtain after some calculation:
frame) we send a light signal from one clock (at the origin) to the other and bounce it back.
Then we obtain after some calculation: