To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Length contraction
Length contraction, according to the special theory of relativity, which was formulated in the early twentieth century through the seminal work of Einstein, Poincaré and Lorentz, is the physical phenomenon of a decrease in length detected by an observer in objects that travel at any non-zero velocity relative to that observer. These contractions (more formally called Fitzgerald-Lorentz contractions or Lorentz-Fitzgerald contractions) only become noticeable, however, at substantial fractions of the speed of light; and the contraction is only in the direction parallel to the direction in which the observed body is travelling. It is important to note that this effect is negligible at everyday speeds, and can be ignored for all regular purposes. It is only when an object approaches speeds on the order of 30,000,000 m/s, i.e. 1/10 of the speed of light, that it becomes important. As the magnitude of the velocity approaches the speed of light, the effect becomes dominant, as we can see from the formula: where
Note that in this equation it is assumed that the object is parallel with its line of movement. Also note that for the observer in relative movement, the length of the object is measured by subtracting the simultaneously measured distances of both ends of the object. For more general conversions, see the Lorentz transformations. An observer at rest viewing an object travelling at the speed of light would observe the length of the object in the direction of motion as zero. Among other reasons, this suggests that objects with mass cannot travel at the speed of light. Product highlight
Lorentz–FitzGerald contraction hypothesisThe Lorentz-FitzGerald contraction hypothesis, the more formal name for length contraction was proposed by George Francis FitzGerald and independently proposed and extended by Hendrik Lorentz to explain the negative result of the Michelson-Morley experiment, which attempted to detect Earth's motion relative to the luminiferous aether. After reading a paper by Heaviside that showed how electric and magnetic fields are affected by motion, FitzGerald hit on the idea that when a body moves through space its size changes due to its motion, and that this may explain Michelson and Morley's "null result". FitzGerald suggested the contraction in an 1889 letter to Science, but did not himself see the letter in print, and it attracted no notice until many years later. He did, however, describe the idea to his scientific friends, and Oliver Lodge mentioned it in print in 1892. Lorentz had hit on the idea independently in 1891 and in 1892 showed how such an effect might be expected based on electromagnetic theory and the electrical constitution of matter. When a body moves through space its dimension parallel to the line of motion would, he said, become less by an amount that depended on its speed. If the speed of the body is v and the speed of light is c, then the contraction is in the ratio For Earth moving in its orbit at about 30 km/s (18.5 mile/s), the contraction would amount to about one part in 200,000,000, which would be about 6 cm (2.5 inches) on the diameter of Earth. This small change accounts for Michelson and Morley's negative result by making the source of light and the mirror draw closer together when the system is moving lengthwise. The formula itself suggests that it is impossible for the velocity of objects (v) to surpass the speed of light. Doing so results in a fraction larger than 1; thus a square root of a negative number. Physical origin of length contraction?Length contraction as a physical effect on bodies composed of atoms held together by electromagnetic forces was proposed independently by George Fitzgerald[1] and by Hendrik Lorentz [2]. The following quote from Joseph Larmor is indicative of the pre-Relativity view of the effect as a consequence of James Clerk Maxwell's electromagnetic theory:
The extension of this specific result to a general result was (and is) considered "ad hoc" by many who prefer Einstein's deduction of it from the Principle of Relativity without reference to any physical mechanism. In other words, length contraction is merely a consequence of the postulates of special relativity. To gain a little physical insight on why length contractions occur, consider what those postulates involve: by requiring the speed of light (a quantity dependent on the fundamental properties of space and time) to be invariant in all frames of reference (including ones in motion) one can appreciate that it would require the "distortion" of the measures of length and time. Apparently Lorentz did not agree to the criticism that his proposal was "ad hoc".[4]
The Trouton-Rankine experiment in 1908 showed that length contraction of an object according to one frame, did not cause changes in the resistance of the object in its rest frame. This is in agreement with some current theories at the time (Special Relativity and Lorentz ether theory) but in disagreement with FitzGerald's ideas on length contraction. Relationship to Special RelativityHenri Poincaré was not at first entirely satisfied with the contraction hypothesis. In Science and Hypothesis he commented on the contraction:
The Lorentz-FitzGerald contraction effect is described by Lorentz in paragraph 8 of his paper "Electromagnetic phenomena in a system moving with any velocity smaller than that of light", 1904. [5] The hypothesis was directed specifically towards electrons with the final intent of explaining the unexpected result of the Trouton-Noble experiment and the Michelson-Morley experiment. Lorentz does this in paragraph 10 of the same paper. Albert Einstein derived the Lorentz contraction directly from the Principle of relativity.[6] According to Einstein, early explanation attempts including the Lorentz-Fitzgerald contraction hypothesis had been "ad-hoc". Lorentz did not agree as can be seen from his draft letter of 1915 to Einstein:
Lorentz later believed that relativity had introduced some doubt about whether the length contraction was apparent or real. In his view "... there can be no question about the reality of the change of length ... [rod II] will be shorter than [rod I], just as it would be if it were kept at a lower temperature ..."[8] A trigonometric effect?
The modern view[citation needed] is that the so-called "Lorentz contraction" is essentially a geometric, in fact a trigonometric phenomenon, which is analogous to something which happens when we consider parallel slices through a cuboid before and after a rotation in E3 (see left half figure at the right). This is the euclidean analog of boosting a cuboid in E1,2. In the latter case, however, we can interpret the boosted cuboid as the world slab of a moving plate. Special relativity concerns relativistic kinematics. Poincaré transformations are a class of affine transformations which can be characterized as the transformations between alternative Cartesian coordinate charts on Minkowski spacetime corresponding to alternative states of inertial motion (and different choices of an origin). Lorentz transformations are Poincaré transformations which are linear transformations (preserve the origin). Lorentz transformations play the same role in Minkowski geometry (the Lorentz group forms the isotropy group of the self-isometries of the spacetime) which are played by rotations in euclidean geometry. Indeed, special relativity largely comes down to studying a kind of noneuclidean trigonometry in Minkowski spacetime, as suggested by the following table:
References
See also
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Length_contraction". A list of authors is available in Wikipedia. |


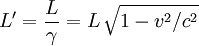
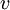 is the relative velocity between the observer and the moving object,
is the relative velocity between the observer and the moving object,
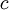 is the
is the 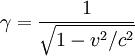 is the Lorentz factor.
is the Lorentz factor.