To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
KMS stateThe statistical mechanics of quantum field theory (see thermal quantum field theory) at the inverse temperature β and chemical potential μ can be characterized by a condition called the KMS condition. Product highlightPreliminariesThe simplest case to study is that of a finite-dimensional Hilbert space, in which one does not encounter complications like phase transitions or spontaneous symmetry breaking. The density matrix of a thermal state is given by where H is the Hamiltonian operator and N is the particle number operator (or charge operator, if we wish to be more general) and is the partition function. We assume that N commutes with H, or in other words, that particle number is conserved. In the Heisenberg picture, the density matrix does not change with time, but the operators are time-dependent. In particular, translating an operator A by τ into the future gives the operator
A combination of time translation with an internal symmetry "rotation" gives the more general A bit of algebraic manipulation shows that the expected values for any two operators A and B and any real τ (we are working with finite-dimensional Hilbert spaces after all). We used that fact that the density matrix commutes with any function of (H-μN) and that the trace is cyclic. As hinted at earlier, with infinite dimensional Hilbert spaces, we run into a lot of problems like phase transitions, spontaneous symmetry breaking, operators which aren't trace class, divergent partition functions, etc.. The complex functions of z, and exist. However, we can still define a KMS state as any state satisfying with
This gives the right large volume, large particle number thermodynamic limit. If there is a phase transition or spontaneous symmetry breaking, the KMS state isn't unique. The density matrix of a KMS state is related to unitary transformations involving time translations (or time translations and an internal symmetry transformation for nonzero chemical potentials) via the Tomita-Takesaki theory. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "KMS_state". A list of authors is available in Wikipedia. |





![\rho_{\beta,\mu}=\frac{e^{-\beta \left(H-\mu N\right)}}{Tr\left[ e^{-\beta \left(H-\mu N\right)} \right]}=\frac{e^{-\beta \left(H-\mu N\right)}}{Z(\beta,\mu)}](images/math/1/6/b/16bc27f995e5ed54d8da4222aac4c227.png)
![Z(\beta,\mu)\ \stackrel{\mathrm{def}}{=}\ Tr\left[ e^{-\beta \left(H-\mu N\right)} \right]](images/math/5/b/b/5bbf28a6bf6994edf6d20c1329037e20.png)
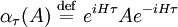 .
.
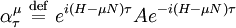
![\langle\alpha^\mu_\tau(A)B\rangle_{\beta,\mu}=Tr\left[\rho \alpha^\mu_\tau(A)B\right]=Tr\left[\rho B \alpha^\mu_{\tau+i\beta}(A)\right] =\langle B\alpha^\mu_{\tau+i\beta}(A)\rangle_{\beta,\mu}](images/math/3/5/e/35edd388fcc76e74eb1db03a8c019aeb.png)
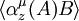 and
and 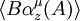 converge if
converge if 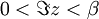 if we make certain technical assumptions like the spectrum of H-μN is bounded from below and its density doesn't increase exponentially (see
if we make certain technical assumptions like the spectrum of H-μN is bounded from below and its density doesn't increase exponentially (see ![\frac{d}{dz}\langle\alpha^\mu_z(A)B\rangle=i\langle\alpha^\mu_z\left(\left[H-\mu N,A\right]\right)B\rangle](images/math/d/d/f/ddfdd6bdcd96810c20053e24c19c5c7d.png)
![\frac{d}{dz}\langle B\alpha^\mu_z(A)\rangle = i\langle B\alpha^\mu_z\left(\left[H-\mu N,A\right]\right)\rangle](images/math/7/1/9/719a0247f95133c798cee8943d95826a.png)
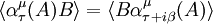
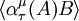 and
and 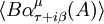 are the boundary distribution values of the analytic functions in question.
are the boundary distribution values of the analytic functions in question.


