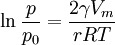Kelvin equation

Kelvin equation describes the change of vapour pressure over liquid curved with a radius r (for example, in a capillary or over a droplet). The Kelvin equation is used for determination of pore size distribution of a porous medium using adsorption porosimetry.

Where:
p - actual vapour pressure 

p0 - saturated vapour pressure

γ - surface tension

Vm - molar volume

R - universal gas constant

r - radius of the droplet

T - temperature

Additional recommended knowledge

How to quickly check pipettes?

Safe Weighing Range Ensures Accurate Results

Daily Visual Balance Check

Equilibrium vapor pressure depends on droplet size. If p₀ < p, then liquid evaporates from the droplets.

If p₀ >p , then the gas condenses onto the droplets… and they grow.

As r increases, p decreases and the droplets grow into bulk liquid.

If we now cool the vapour, then T decreases, but so does p₀ . This means p/p₀ increases as the liquid is cooled. We can treat γ and V as approximately fixed, which means that the critical radius r must also decrease. The further you supercool a vapour, the smaller the critical radius becomes. Ultimately it gets as small as a few molecules and the liquid undergoes homogeneous nucleation and growth.

See also

• Condensation

References

• W. T. Thomson, Phil. Mag. 42, 448 (1871)
• S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, 2nd edition,Academic Press, New York, (1982) p.121
• Adamson and Gast, Physical Chemistry of Surfaces, 6th edition, (1997) p.54