Kozeny-Carman equation

The Kozeny-Carman equation is a relation used in the field of fluid dynamics to calculate the pressure drop of a fluid flowing through a packed bed of solids. The equation is only valid for laminar flow.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

How to ensure accurate weighing results every day?

Daily Sensitivity Test

Equation

The equation is given as^[1]:

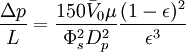
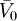where Δp is the pressure drop, L is the total height of the bed, is the superficial or "empty-tower" velocity, μ is the viscosity of the fluid, ε is the porosity of the bed, Φ_s is the sphericity of the particles in the packed bed, and D_p is the diameter of the related spherical particle^[2].

This equation holds for flow through packed beds with particle Reynolds numbers up to approximately 1.0, after which point frequent shifting of flow channels in the bed causes considerable kinetic energy losses.

This equation can be expressed as '"flow is proportional to the pressure drop and inversely proportional to the fluid viscosity'", which is known as Darcy's law^[1].

References

1. ^ ^{a b} McCabe, Warren L.; Smith, Julian C. & Harriot, Peter (2005), (seventh ed.), New York: McGraw-Hill, pp. 163-165, ISBN 0-07-284823-5
2. ^ McCabe, Warren L.; Smith, Julian C. & Harriot, Peter (2005), (seventh ed.), New York: McGraw-Hill, pp. 188-189, ISBN 0-07-284823-5

See also

• Fractionating column
• Raschig ring