To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Linear polarizationIn electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation. See polarization for more information. Product highlightHistorically, the orientation of a polarized electromagnetic wave has been defined in the optical regime by the orientation of the electric vector, and in the radio regime, by the orientation of the magnetic vector. Mathematical description of linear polarizationThe classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is (cgs units) for the magnetic field, where k is the wavenumber, is the angular frequency of the wave, and c is the speed of light. Here is the amplitude of the field and is the Jones vector in the x-y plane. The wave is linearly polarized when the phase angles
This represents a wave polarized at an angle θ with respect to the x axis. In that case the Jones vector can be written
The state vectors for linear polarization in x or y are special cases of this state vector. If unit vectors are defined such that and then the polarization state can written in the "x-y basis" as
References
See alsoThis article contains material from the Federal Standard 1037C, which, as a work of the United States Government, is in the public domain. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Linear_polarization". A list of authors is available in Wikipedia. |





![\mathbf{E} ( \mathbf{r} , t ) = \mid \mathbf{E} \mid \mathrm{Re} \left \{ |\psi\rangle \exp \left [ i \left ( kz-\omega t \right ) \right ] \right \}](images/math/f/0/7/f07592ed67ae0ecb6ebb466182fcfbde.png)
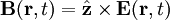
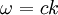
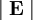
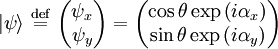
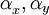 are equal,
are equal,
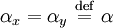 .
.
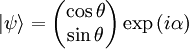 .
.
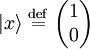
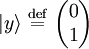
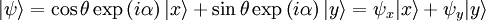 .
.


