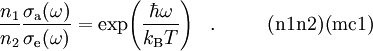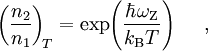To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
McCumber relation
Product highlight
DefinitionLet σa(ω) and the emission cross-section σe(ω) be effective absorption and emisison cross-sections at frequency ω, and let
where GainIt is typical, that the lasing properties of a medium are determined by the temperature and the population at the excited laser level, and are not sensitive to the way of excitation, used to achieve a given population at the upper laser level. In this case, the absorption cross-section
σa(ω)
and the emission cross-section
σe(ω)
at frequency
D.E.McCumber had postulated this properties, and found that the emisison and absorption cross-sections are not independent [1][2]; they are related with Equation (1). Idealized atomsIn the case of an idealized two-level atom, the consideration of the detailed balance for the emission and absorption, that preserves the Max Planck formula for the black body radiation leads to equality of cross-section of absorption and emission. In the solid-state lasers, the splitting of each of laser levels leads to the broadening which greatly exceeds the natural spectral linewidth. In the case of an ideal two-level atom, the product of the linewidth and the lifetime is of order of unity, which follows to the Heisenberg uncertainty principle. In the solid-state laser materials, the linewidth is several orders of magnitude larger. Therefore, the spectra of emission and absorption are determined with distribution of excigtation among sublevels rather than by the shape of the spectral line of each individual transition between sublevels. This distribution is determined by the effectie temperature within each of laser levels. The hypothesis of McCumber is that the distribution of excitation among sublevels is termal. Then, the effectie temperature[5] determines the spectra of emission and absorption. Deduction of the McCumber relationConsider the set of active centers (fig.1.). Assime fast transition between sublevels within each level, and slow transition between levels. According to the McCumber hypothesis, the corss-sections σa and σe do not depend on the populations N1 and N2. Therefore, we can deduce the relation, assumnig the thermal state. Let The product
Rewrite it as
The thermal distribution of density of photons follows from blackbody radiation [6]
Both (4) and (5) hold for all frequencies For each site number
Neglecting the cooperative coherent effects, the emission is additive:
for any concentration
Then, the comparison of (D1) and (D2) gives the relation
This relation is equivalent of the McCumber relation (mc), if we define the zero-line frequency ωZ as solution of equation
the subscript
Then, (n1n2) becomes equivalent of the McCumber relation (mc). We see, no specific property of sublevels of active medium is required to keep the McCumber relation. It follows from the assumption about quick transfer of energy among excited laser levels and among lower laser levels. The McCumber relation (mc) has the same range of validity, as the concept of the emission cross-section itself. Confirmation of the McCumber relationThe McCumber relation is confirmed for various media [7][8]. In particular, relation (1) allows to approximate two functions of frequency, emission and absorption cross sections, with single fit [9]. Violation of the McCumber relation and perpetual motion
Y.2006, the strong violation of McCumber relation was observed for Yb:Gd2SiO5 and reported in 3 independent journals[10][11][12]. Typical behaivor of the cross-sections is shown in FIg.2 with thick curves. The emission cross-section is practically zero at wavelength 975nm; this property makes Yb:Gd2SiO5 an excellent material for efficient solid-state lasers. The project of a Perpetual motion was suggested basing on these prpoperties. It is sufficient to fill a box with reflecting walls with Yb:Gd2SiO5, and allow it to exchange radiation with a blackbody through the spectrally-selective window, which is transparent in vicinity of 975nm, and reflector at other wavelengths. Due to the lack of emissivity at 975nm, the medium should warm, breaking the thermal equilibrium. Unfortunately, this brilliant opportunity was closed in 2007; the correction of the effective emission cross section (black thin cirve) was suggested [3] and confirmed[13]. References
Categories: Spectroscopy | Solid-state lasers |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "McCumber_relation". A list of authors is available in Wikipedia. |





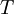 be the effective temperature of the medium. The McCumbner relation is
be the effective temperature of the medium. The McCumbner relation is
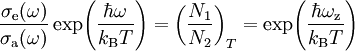
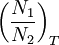 is thermal steady-state ratio of populations; frequensy
is thermal steady-state ratio of populations; frequensy 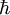 is the Planck constant and
is the Planck constant and
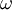 .
.
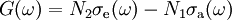
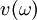 be croup velocity of light in the medium.
be croup velocity of light in the medium.
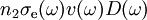 is spectral rate of
stimulated emission, and
is spectral rate of
stimulated emission, and 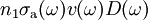 is that of absorption;
is that of absorption; 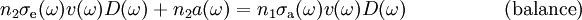
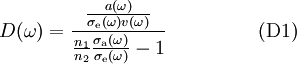
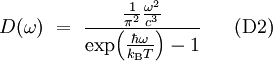
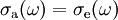 , and
, and 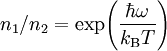 ,
which leads to the relation between the spectral rate of spontaneous emission
,
which leads to the relation between the spectral rate of spontaneous emission
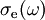
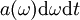 ,
which is probability of emission of a photon within small spectral interval
,
which is probability of emission of a photon within small spectral interval
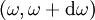 during a short time interval
during a short time interval 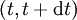 , assuming that at time
, assuming that at time 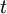 the atom is excited.)
The relation (D2) is fundamental property of spontaneous and stimulated emission,
and, perhaps, the only way to prohibit a spontaneous break of the thermal equilibrium in the thermal state of
excitations and photons.
the atom is excited.)
The relation (D2) is fundamental property of spontaneous and stimulated emission,
and, perhaps, the only way to prohibit a spontaneous break of the thermal equilibrium in the thermal state of
excitations and photons.
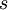 , for each sublevel number
, for each sublevel number 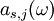 can be expressed from consideration of idealized two-level atoms
can be expressed from consideration of idealized two-level atoms

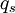 of sites and for any partial population
of sites and for any partial population 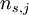 of sublevels, the same proportionality between
of sublevels, the same proportionality between 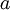 and
and 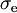 holds for the effective cross-sections:
holds for the effective cross-sections: