To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Microstate (statistical mechanics)In statistical mechanics, a microstate describes a specific detailed microscopic configuration of a system, that the system visits in the course of its thermal fluctuations. In contrast, the macrostate of a system refers to its macroscopic properties such as its temperature and pressure. In statistical mechanics, a macrostate is characterized by a probability distribution on a certain ensemble of microstates. This distribution describes the probability of finding the system in a certain microstate as it is subject to thermal fluctuations. Let us now turn to the case of large systems: even if those systems are theoretically able to fluctuate between very different microstates, observing such a fluctuation becomes less and less likely as the size of the system increases. This makes up for the thermodynamic limit. In this limit, the microstates visited by a system during its fluctuations all have the same bulk (or macroscopic) properties. Product highlight
Microscopic definitions of thermodynamic conceptsThe definitions of this section link the thermodynamic properties of a system to its distribution on its ensemble (or set) of microstates. Note that all definitions and expressions of this section are valid even far away from thermodynamic equilibrium. In this article we will consider a system which is distributed on an ensemble of N microstates. pi is the probability associated to the microstate i, and Ei is its energy. Here microstates form a discrete set, which means we are working in quantum statistical mechanics, and Ei is an energy level of the system. Internal energyThe internal energy is the mean of the system's energy This definition is the traduction of the first law of thermodynamics. EntropyThe absolute entropy exclusively depends on the probabilities of the microstates. Its definition is the following:
where kB is Boltzmann's constant Entropy evaluates according to the second law of thermodynamics. The third law of thermodynamics is consistent with this definition, since an absolute entropy of 0 means that the macrostate of the system reduces to a single microstate. Heat and workWork is the energy transfer associated to the effect of an ordered, macroscopic action on the system. It is not possible to cause a jump in energy level of a microscopic component of a system through the direct effect of work, but it is possible to change the energy of the system's energy levels. On the other hand heat is the energy transfer associated with a disordered, microscopic action on the system, associated to jumps in energy levels for the microscopic components of the system. The microscopic definitions of heat and work are the following: So that Examples: Warning: the two above definitions of heat and work are among the few expressions of statistical mechanics where the sum corresponding to the quantum case cannot be converted into an integral in the classical limit of a microstate continuum. The reason is that classical microstates are usually not defined in relation to a precise associated quantum microstate, which means that when work changes the energy associated to the energy levels of the system, the energy of classical microstates doesn't follow this change. See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Microstate_(statistical_mechanics)". A list of authors is available in Wikipedia. |





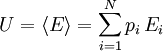
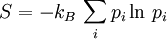 ,
,